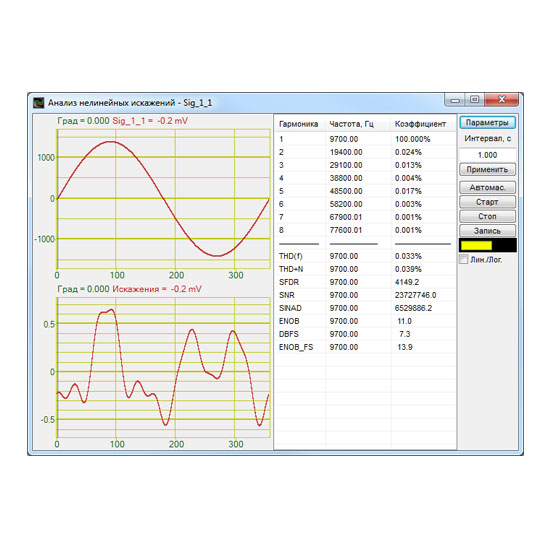
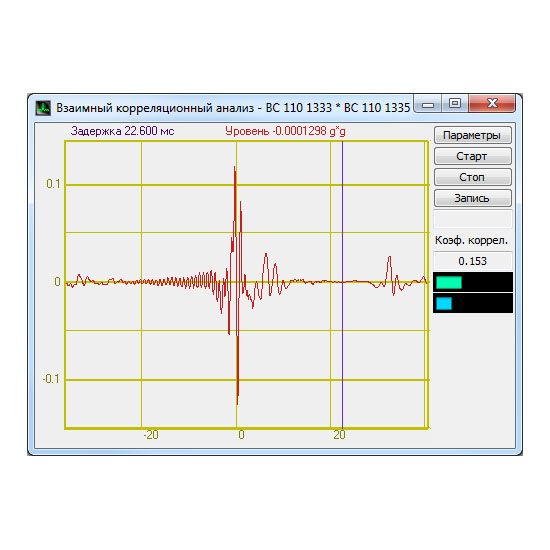
Виртуальные приборы ZETLAB
Программное обеспечение ZETLAB — это виртуальная лаборатория, предоставляющая пользователю мощные средства для визуализации, спектрального анализа, измерения электрических параметров, генерации, записи и воспроизведения сигналов. Виртуальные приборы ZETLAB предназначены для решения задач измерения и управления в области сейсмики, вибрации, термометрии, тензометрии и т.д. Программы из состава ZETLAB обрабатывают сигналы, поступающие на входные каналы анализаторов спектра, сейсмостанций, тензостанций, модулей АЦП ЦАП. Также устройства и программное обеспечение ZETLAB легко интегрируются с инфраструктурой OPC.
Программное обеспечение ZETLAB регулярно обновляется и дополняется. Всем пользователям обновления доступны абсолютно бесплатно. Порядок обновления ПО описан в разделе Обновление программного обеспечения.
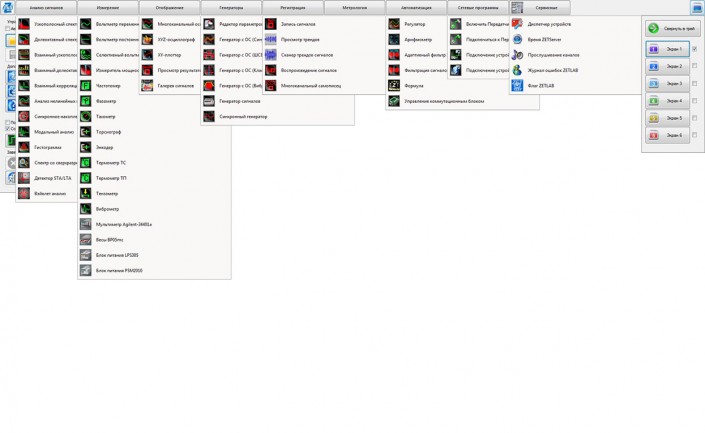
Ниже приведен полный перечень виртуальных приборов ZETLAB.
Анализ сигналов
Измерение параметров сигналов
Отображение
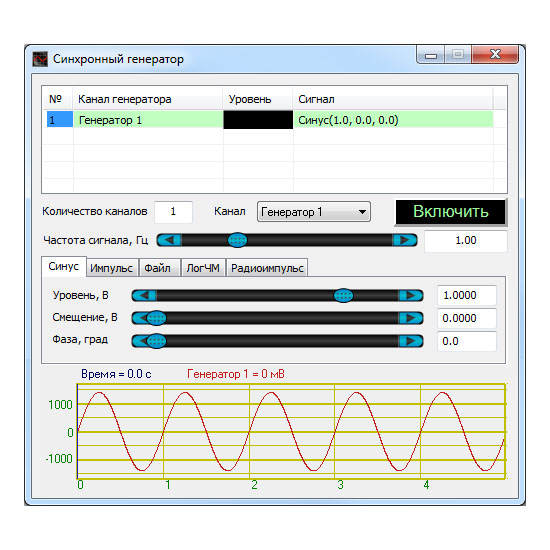
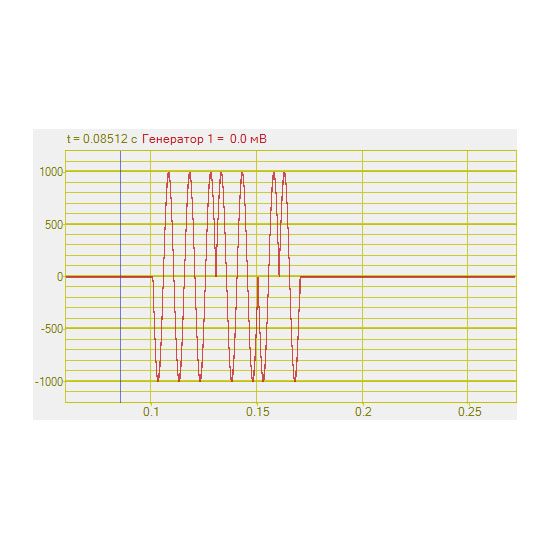
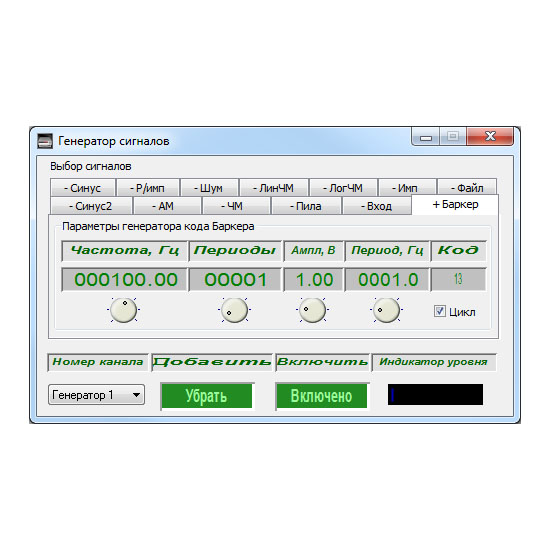
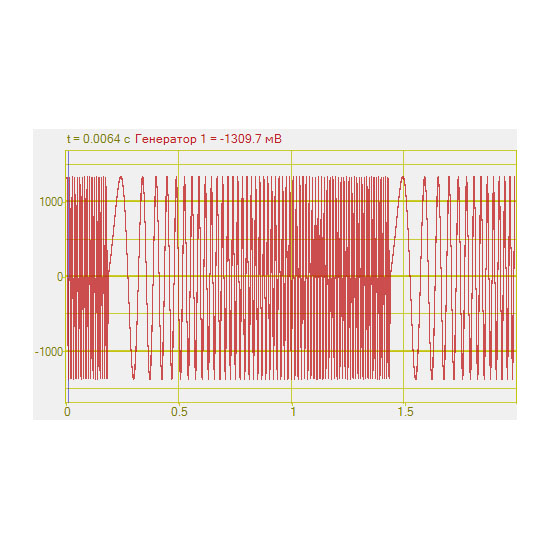
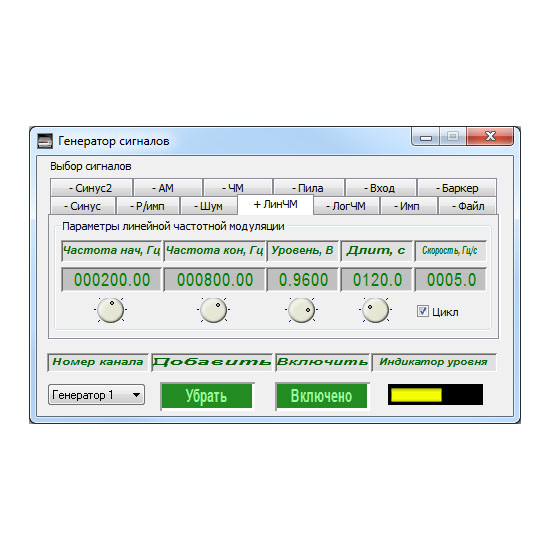
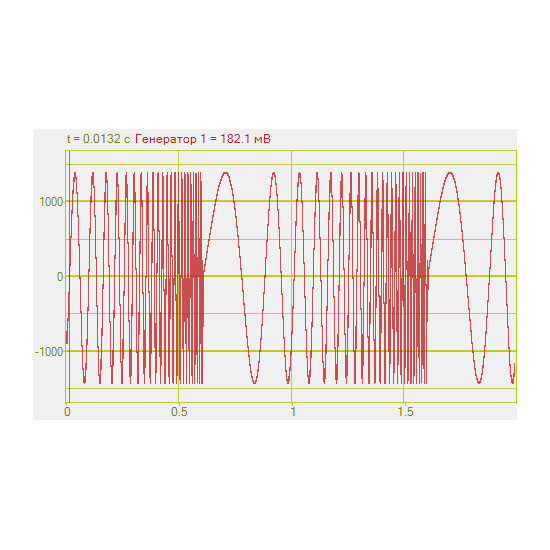
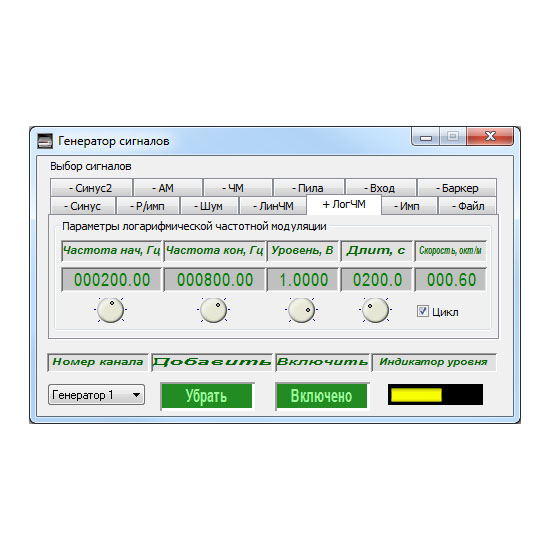
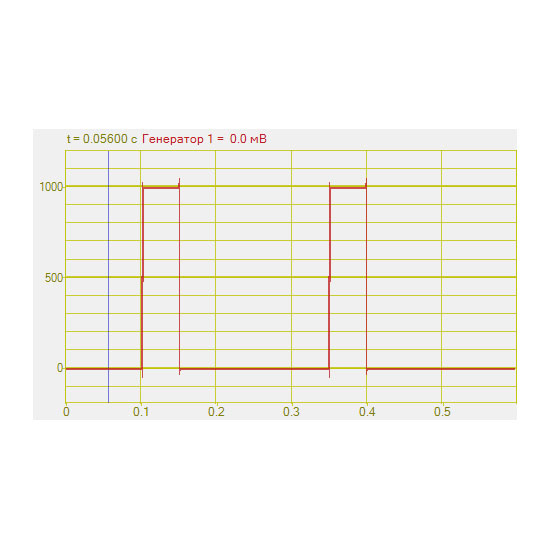
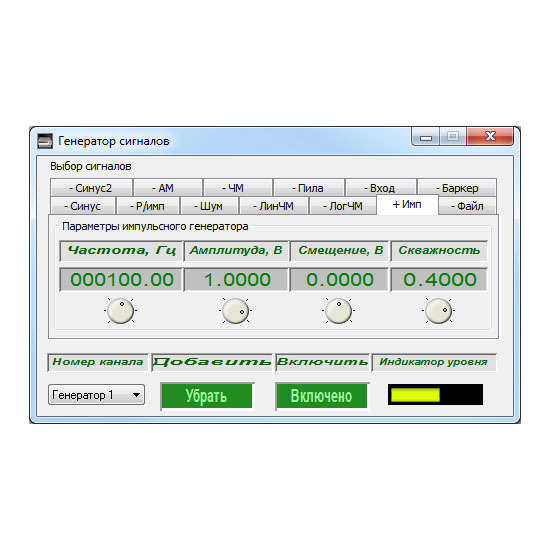
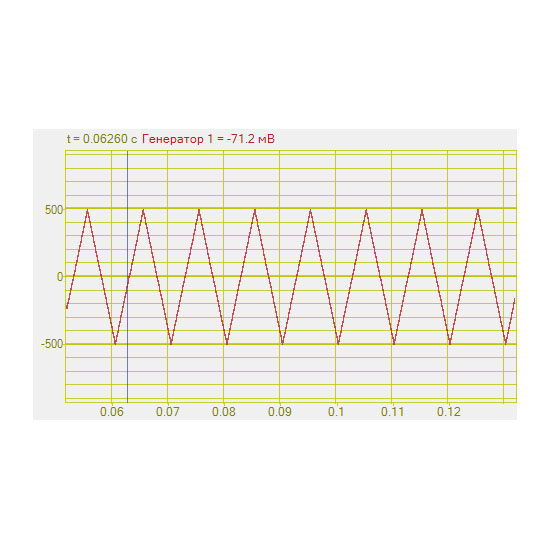
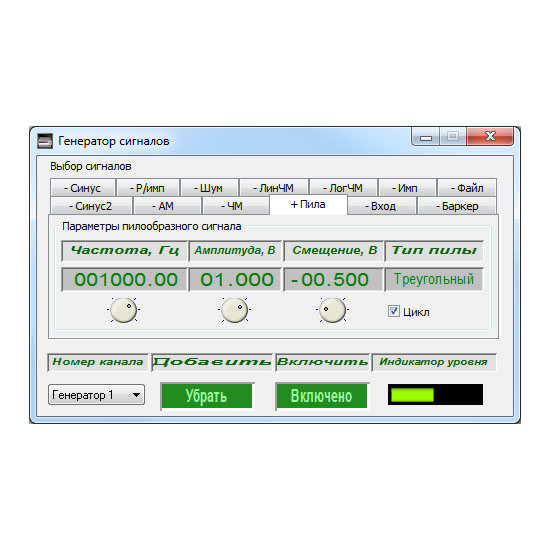
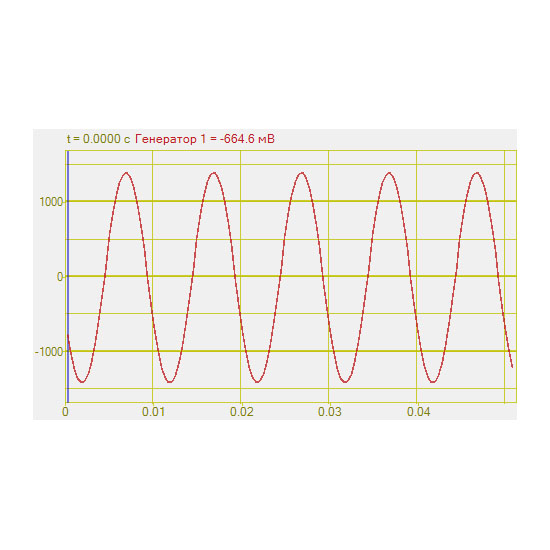
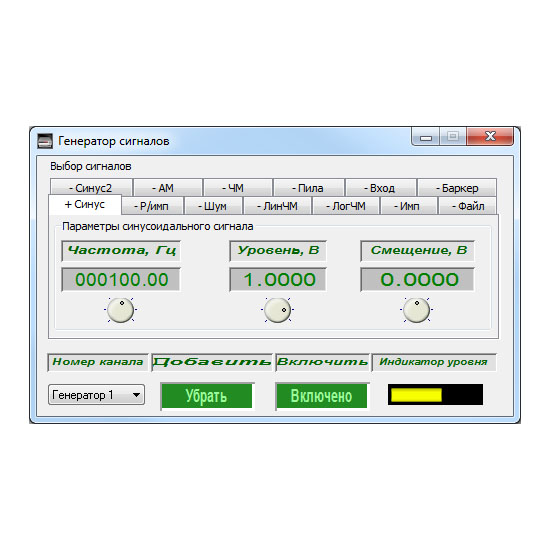
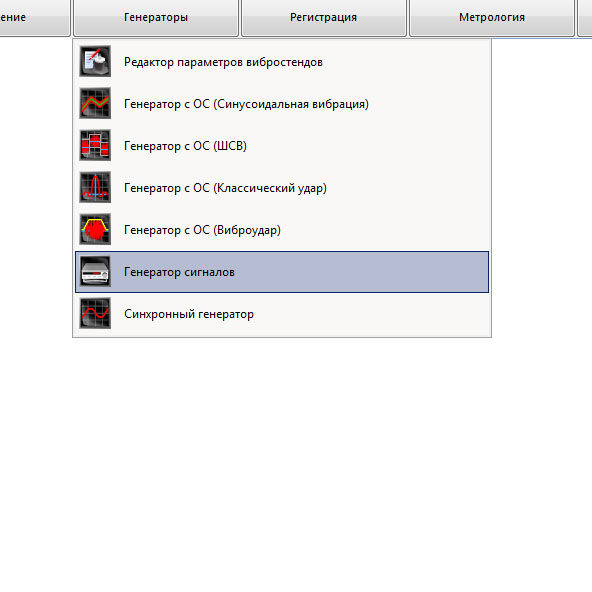
Генераторы
Регистрация
Автоматизация
Сетевые
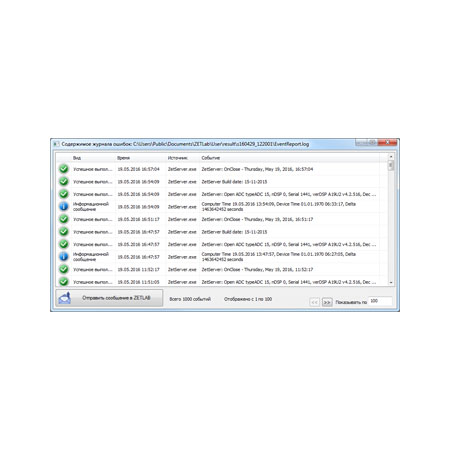
Сервисные
ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
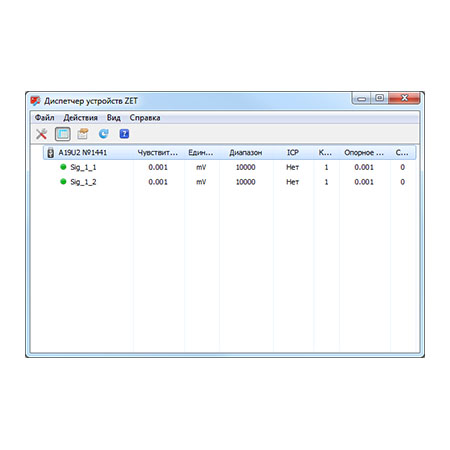
Об изменении параметров измерительных каналов при обработке...
Все измерительные каналы, доступные для обработки, имеют определенный набор параметров. Основные параметры это:
- Частота дискретизации канала (FADC)
- Минимальное измеряемое значение (VALMIN)
- Максимальное измеряемое значение (VALMAX)
- Разрешающая способность (VALSUB)
- Опорное значение для расчета относительной величины в дБ (REF)
- Размерность данных (DIM)
Частота дискретизации представляется в Гц. Минимальное и максимальное измеряемые значения данных, а разрешающая способность и опорное значение имеют размерность данных DIM. Разрешающая способность и опорное значение должны быть положительными числами.
При оцифровке аналогового сигнала акселерометра BC 1313 с помощью регистратора ZET 048 с частотой дискретизации 100 Гц оцифрованные каналы X, Y, Z будут иметь следующие параметры:
FADC = 100; VALMIN = -20; VALMAX = 20; VALSUB = 2•10-5; REF = 0,0003; DIM = м/с2
Не всегда VALMIN= — VALMAX. Так, например, при измерении температуры тела человека с помощью ртутного медицинского термометра, в быту называемого градусником, VALMIN = 34,5°С, VALMAX= 42°С.
При отображении значений в дБ параметры станут следующими:
FADC = 100; VALMIN = -15,6; VALMAX = 96,5; VALSUB = 0,01; REF = 1; DIM = дБ
В этом случае новые значения рассчитываются по формулам:
![]()
![]()
Разрешающая способность величин, отображаемых в дБ, всегда приравнивается 0.01 дБ, величина REF приравнивается 1. дБ от дБ не рассчитываются.
Если любой из вышеупомянутых X, Y, Z каналов преобразовать с помощью алгоритма вольтметра постоянного тока со временем усреднения 1 сек, то получаются несколько другие параметры нового канала:
FADC = 1; VALMIN = -20; VALMAX = 20; VALSUB = 2•10-6; REF = 0,0003; DIM = м/с2
Изменилась частота дискретизации и разрешающая способность данных. Период следования новых данных — это время усреднения, т. е. 1 сек, следовательно, частота дискретизации новых данных равна 1 Гц. Т.к. один отчет новых данных получается путем усреднения N = 100 отсчётов исходных данных (N = 100 Гц * 1 сек), то разрешающая способность уменьшилась в √N, т.е. в 10 раз (см. ГОСТ Р 8.736-2011).
Если вместо алгоритма вольтметра постоянного тока использовать алгоритм вольтметра переменного тока, который вычисляет среднее СКЗ (корень квадратный из среднего квадрата величины), то новые данные будут иметь следующие параметры:
FADC = 1; VALMIN = 0; VALMAX = 20 / 1,4; VALSUB = 2•10-6/1,4; REF = 0,0003; DIM = м/с2
Максимальное значение и разрешающая способность данных уменьшилось в √2 (приблизительно 1,4). Минимальное значение стало равно нулю.
Более сложные изменения в значениях параметров каналов будут при выполнении цифрового дифференцирования и цифрового интегрирования. Вначале предположим, что исходный сигнал является гармоническим сигналом с частотой f, тогда можно записать:
![]() ,
,
где w = 2•π•f — круговая частота,
![]()
![]()
Получаем, что при дифференцировании величина сигнала как бы умножается на коэффициент, равный круговой частоте. А при интегрировании — делится на такую же величину.
Для широкополосного сигнала в полосе от f1 до f2 (круговая частота от w1 до w2) для дифференцирования максимальное значение может увеличиться в w2 раз, а минимальное значение разрешающей способности может быть изменено в w1 раз. При этом для интегрирования максимальное значение может увеличиться в 1/w1 раз, а минимальное значение разрешающей способности может быть изменено в 1/w2 раз.
При цифровой обработке сигналов можно считать:
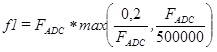
f2 = 0,5•FADC
Поэтому при дифференцировании параметры канала станут следующими:
FADC = 100; VALMIN = -6283; VALMAX = 6283; VALSUB = 1,6•10-5; REF = 0,0003; DIM = м/с3,
а при интегрировании:
FADC = 100; VALMIN = -16; VALMAX = 16; VALSUB = 6•10-8; REF = 0,0003; DIM = м/с
Следует обратить внимание на очевидные изменения размерности.
Если данные канала вначале будет подвергнуты цифровому дифференцированию, а потом цифровому интегрированию, то параметры результирующего канала, не смотря на очевидность проделанной операции, не станут равны параметрам исходного канала. Но такова специфика ЦОС, и такому результату не следует удивляться и считать это ошибкой.
Важную роль в ЦОС играет спектральный анализ.
Пусть (см. статью в Википедии «Спектральная плотность») у нас есть некоторый случайный процесс x(t), например: некоторое электрическое напряжение, измеряемое в В., тогда полная энергия этого процесса Ех определется как:
![]()
где: функция Sx(f) = |X(f)|2 – спектр мощности, имеющий размерность В2/Гц. Физический смысл произведения Sx(f) на полосу частот df можно трактовать как энергию сигнала в полосе частот от f-df/2 до f+df/2 , поэтому функцию Sx(f) так же называют энергетическим спектром.
В ЦОС спектральной плотностью мощности (СПМ) иногда называют функцию √Sx(f), имеющую размерность В/√Гц. Следует отметить (см. статью в Википедии «Спектральная плотность мощности»), что в спектре плотности мощности есть информация только об амплитудных спектральных составляющих, информация о фазе теряется. Поэтому все сигналы с одинаковым спектром амплитуд, но с различными спектрами фаз имеют одинаковые спектры плотности мощности.
Таким образом, получаем, что при расчёте СПМ сигнала X, Y или Z ВС 1313 (см. выше) при длительности сигнала 1 сек и частотном разрешении 0,1 Гц получаем следующие параметры канала СПМ:
FADC = 1; VALMIN = 0; VALMAX = 60; VALSUB = 6•10-6; REF = 0,0003; DIM = м/с2/√Гц,
где:
20 / √0,1 = 200 • √0,1 ≈ 20 • 0,3 = 60
При расчете дБ следует брать 20 логарифмов от отношения VAL / REF.
При расчёте энергетического спектра параметры будут следующими:
FADC = 1; VALMIN = 0; VALMAX = 3600; VALSUB = 1,2•10-12; REF = 0,0003; DIM = м2/с4/Гц.