Sinusoidal vibration: Interrelation of acceleration, velocity and displacement
In the course of tests performance with the use of harmonic signal (for instance, during calibration of the transducers), it is important to know the relation between vibration displacement, vibration velocity, and vibrational acceleration. If vibration displacement amplitude is S, vibration velocity amplitude is V, and vibration acceleration amplitude is A, then:
| A = S·(2πf)2/103, | V = S·2πf/10, | S = A·103/(2πf)2, |
| where f is amplitude in Hz; А is vibration acceleration in m/s2 V is vibration velocity in cm/s S is the vibration displacement in mm. |
||
For nstance, at the frequency of 50 Hz and with displacement of 1 mm, the velocity value will be 31 cm/s, and the acceleration value – 99 m/s2 respectively.
In order to facilitate calculation of the relevant parameters, we offer you to use the Calculator for vibrational parameters. The calculator enables simple evaluation of the interrelated vibrational parameters. All you have to do is to set the relevant parameter to be calculated, and to enter the available values.
Interrelation between acceleration values:
| g | m/s2 | cm/s2 |
| 1 | 9,81 | 981 |
| 0,102 | 1 | 100 |
| 0,00102 | 0,01 | 1 |
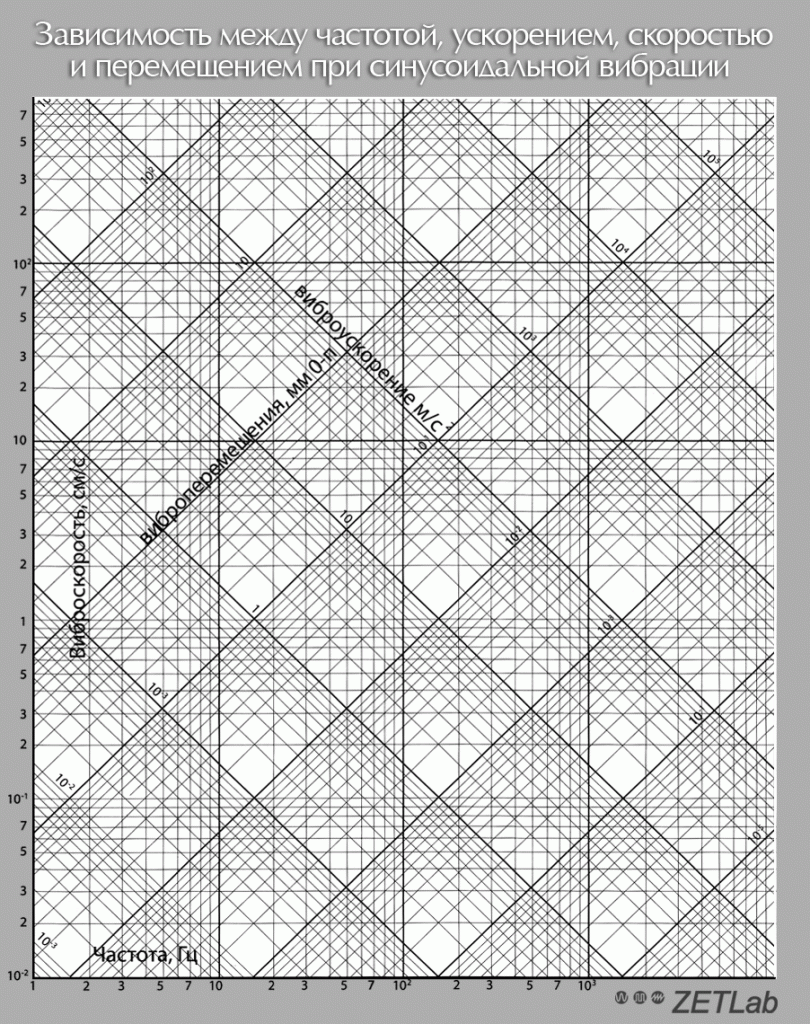
In addition to formulas and calculator, it is also possible to use the nomographic chart, representing the ratio between different parameters of mechanical oscillations, i.e., between frequency, displacement, velocity, and acceleration of harmonic mechanical oscillations. Based on the available values of two parameters, and with the use of the nomographic chart below, you can determine the values of the two remaining parameters of the mechanical oscillations.