Measuring functions
program Formula
Measuring functions are intended for measurements of signals’ various parameters. Just like as for other functions of Formula program, the arguments can be set as equations. 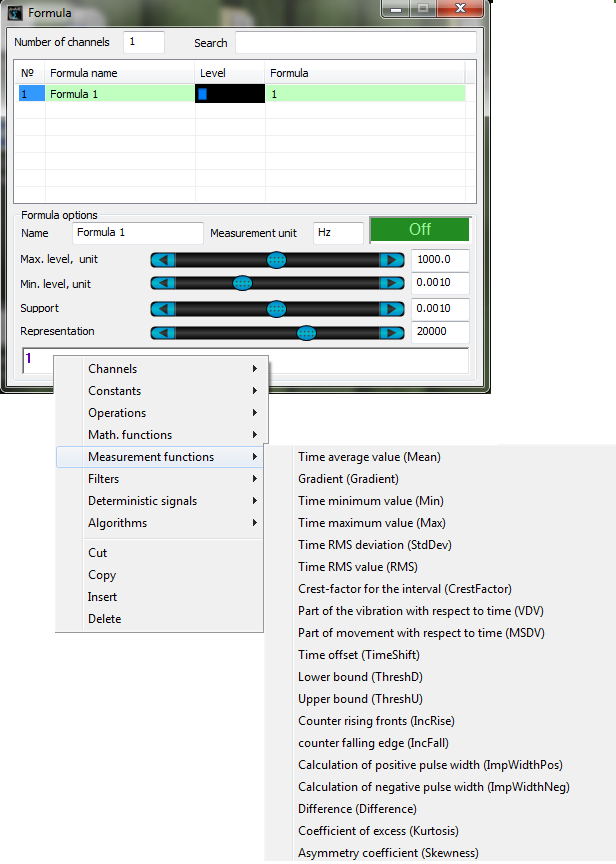
Mean(
Gradient (
Min(
Max(
In fact, these functions can be described as filters with AFR similar to the function sin(x)/x, where x is a reciprocal value of the set time interval. In the case, if this interval duration is more than 0,1 s, the values will be rounded with a precision of 0,1 s to the next larger value in order to accelerate operation and save program memory.
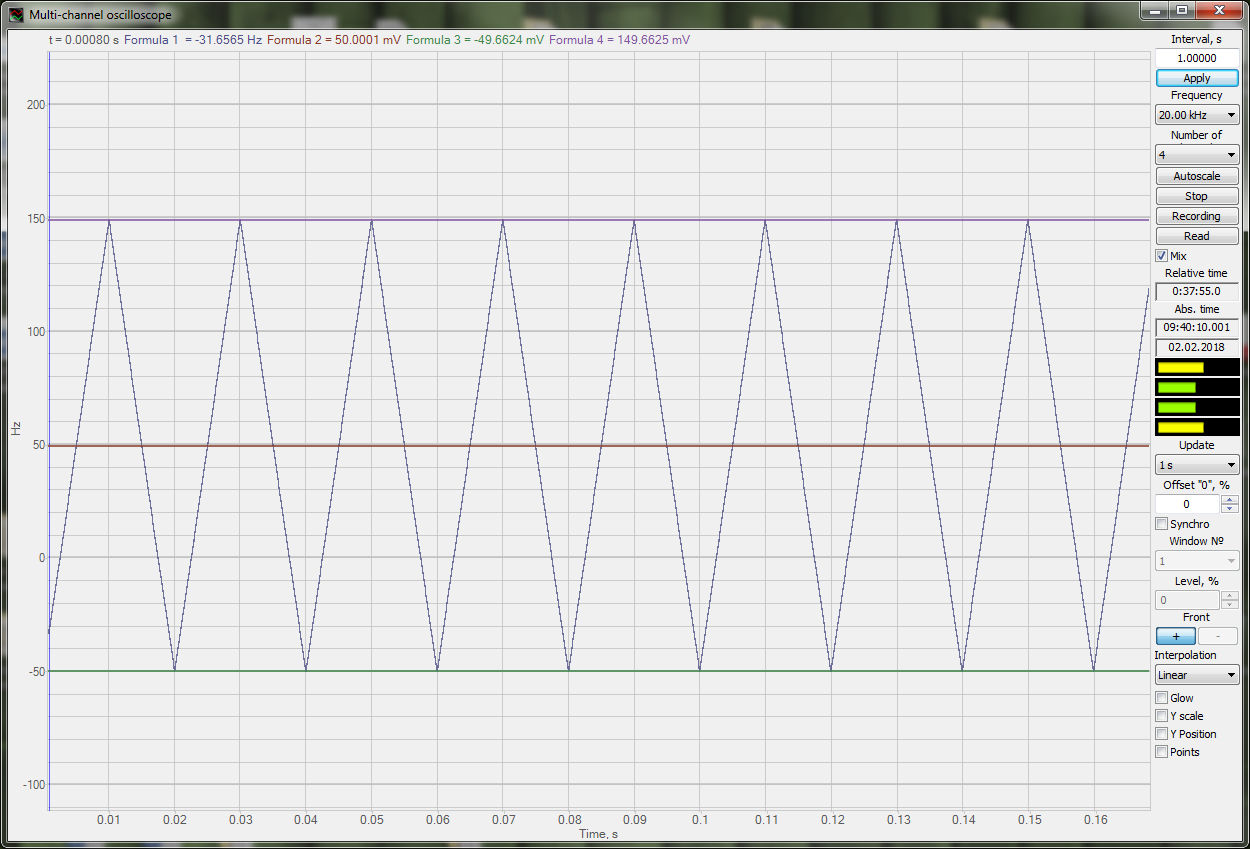
The Figure below shows the calculation of minimal, maximal and average values of the channel. As a signal for analysis, we use a signal of triangular shape. Calculation results are displayed at the oscillograph in the compatibility mode:
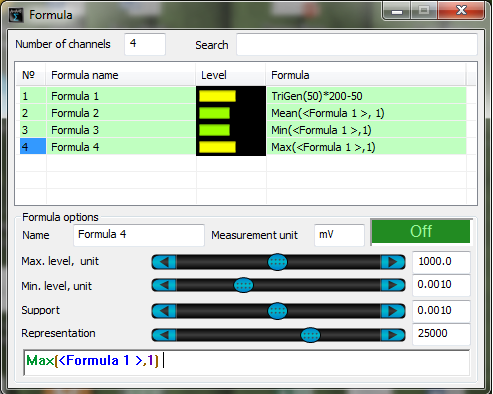
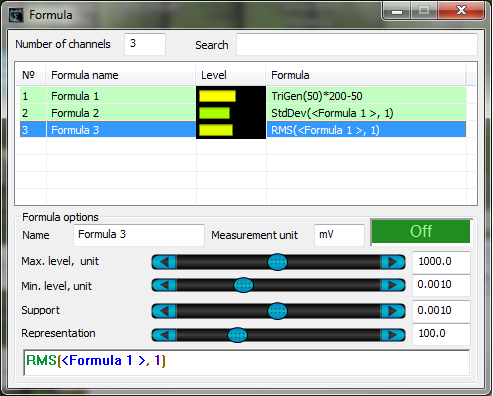
StdDev(
RMS(
The figure below shows the result of functions StdDev and RMS operation, in which as an argument there is used a signal of the same amplitude, but with a different constant component level.
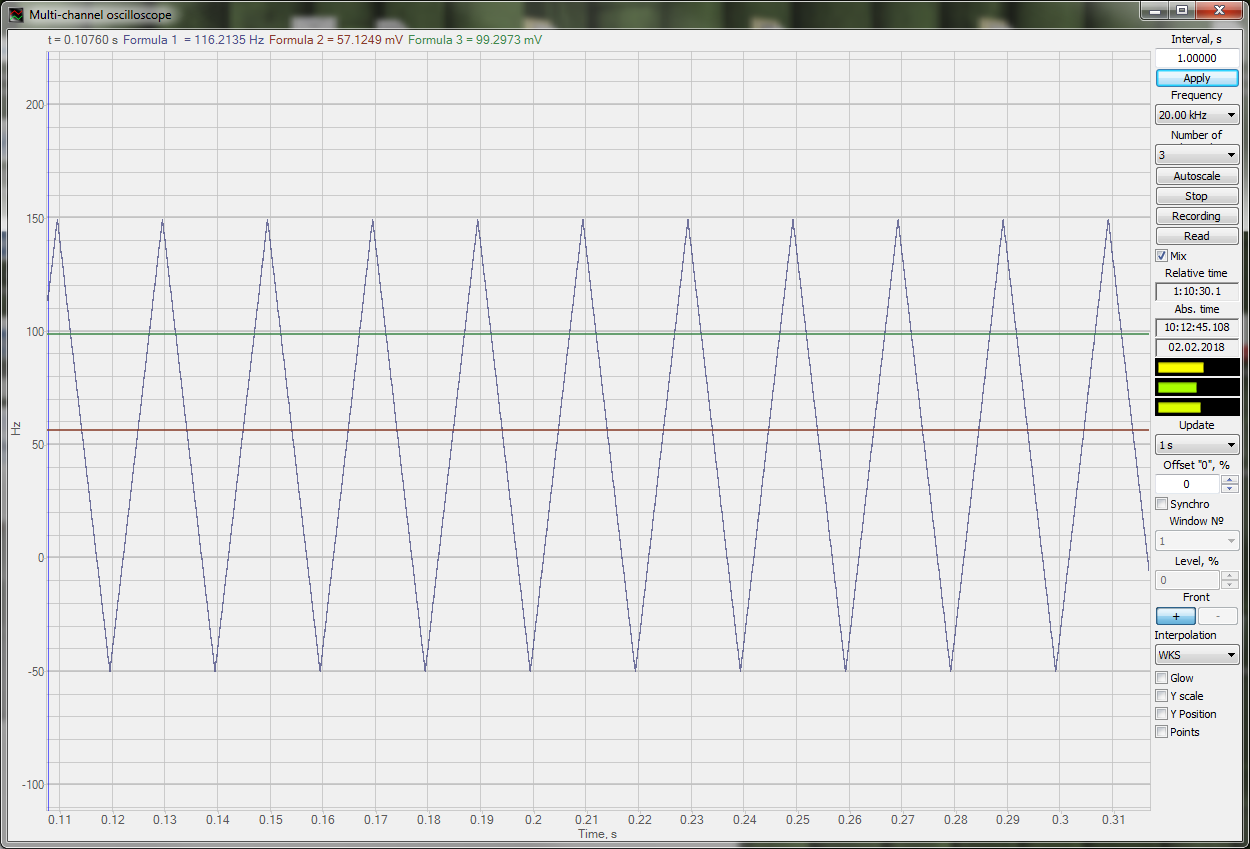
CrestFactor(
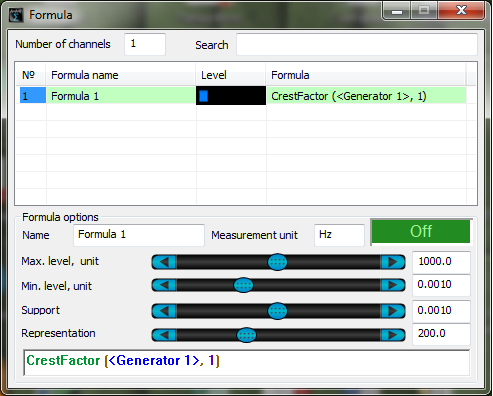
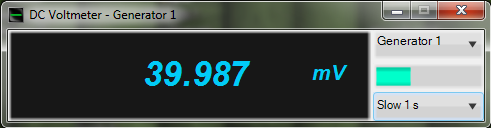
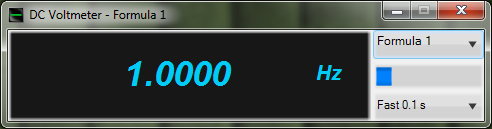
The figure below shows an example of CrestFactor function operation. A sinusoidal signal is used as an argument. Its parameters (RMS and peak value) are measured by DC voltmeter. Operation results of CrestFactor function are displayed by DC voltmeter.
VDV(, t) – vibration dose for time t.
MSDV(, t) – movement dose for time t.
Crest factor (CrestFactor), vibration dose (VDV) and movement dose (MSDV) are the parameters of remedial acceleration:
remedial acceleration RMS aw: translational or angular vibration averaged by time is determined by the formula:
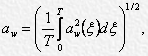
- aw(ξ) – current value of remedial acceleration (translational or angular) as a time function ξ;
- Т – period of measurements.
remedial acceleration level Lw: The level of remedial acceleration RMS, dB, is determined by the formula:
![]()
- aw – remedial acceleration RMS, m/s2;
- а0 – acceleration reference value, 10-6 m/s2.
current RMS value of remedial acceleration текущее aw,θ(t): RMS value of remedial acceleration at moment of time t is determined by the formula:
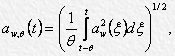
- aw(ξ) -current value of remedial acceleration at the moment of time ξ;
- θ – integration time;
- t – current time.
Note- as an approximation of linear averaging you can use exponential averaging, which is determined by the following formula:
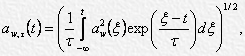
- τ – exponential averaging time constant.
maximum short-term RMS value (of remedial acceleration) MTVV: Maximum value of current RMS value of remedial acceleration for integration period θ, which is equal to 1 second.
movement dose MSDV: Value, represented by remedial acceleration RMS square integral aw(t), m/s1,5, which is determined by the formula:
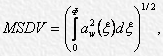
where Ф – is a total period of time during which low-frequency oscillations are observed (these very oscillations cause motion sickness).
Notes:
1 Movement dose can be obtained from RMS value remedial acceleration value by multiplication by the ratio Ф1/2.
2 Unless otherwise specified, impact time Ф is considered to be equal to T.
vibration dose VDV: Value, which represents an integral of remedial acceleration fourth power aw(t), m/s1,75 and is determined by the formula:
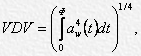
where Ф – is the total duration of vibration impact.
Notes
1. Vibration dose is more sensible to peak acceleration values than the RMS. Доза вибрации более чувствительна к пиковым значениям ускорения, чем среднеквадратичное значение.
2. Unless otherwise specified, impact time Ф is considered to be equal to measurements duration T.
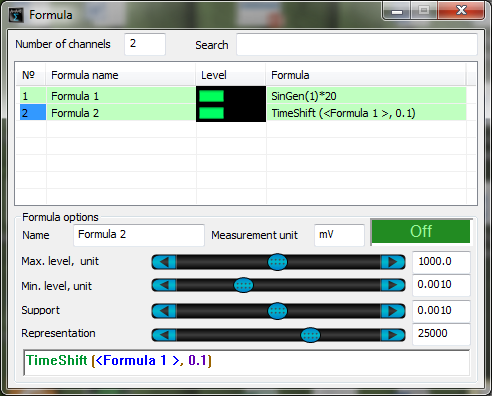
TimeShift (, t) – time shift by the channel, for a particular period in seconds.
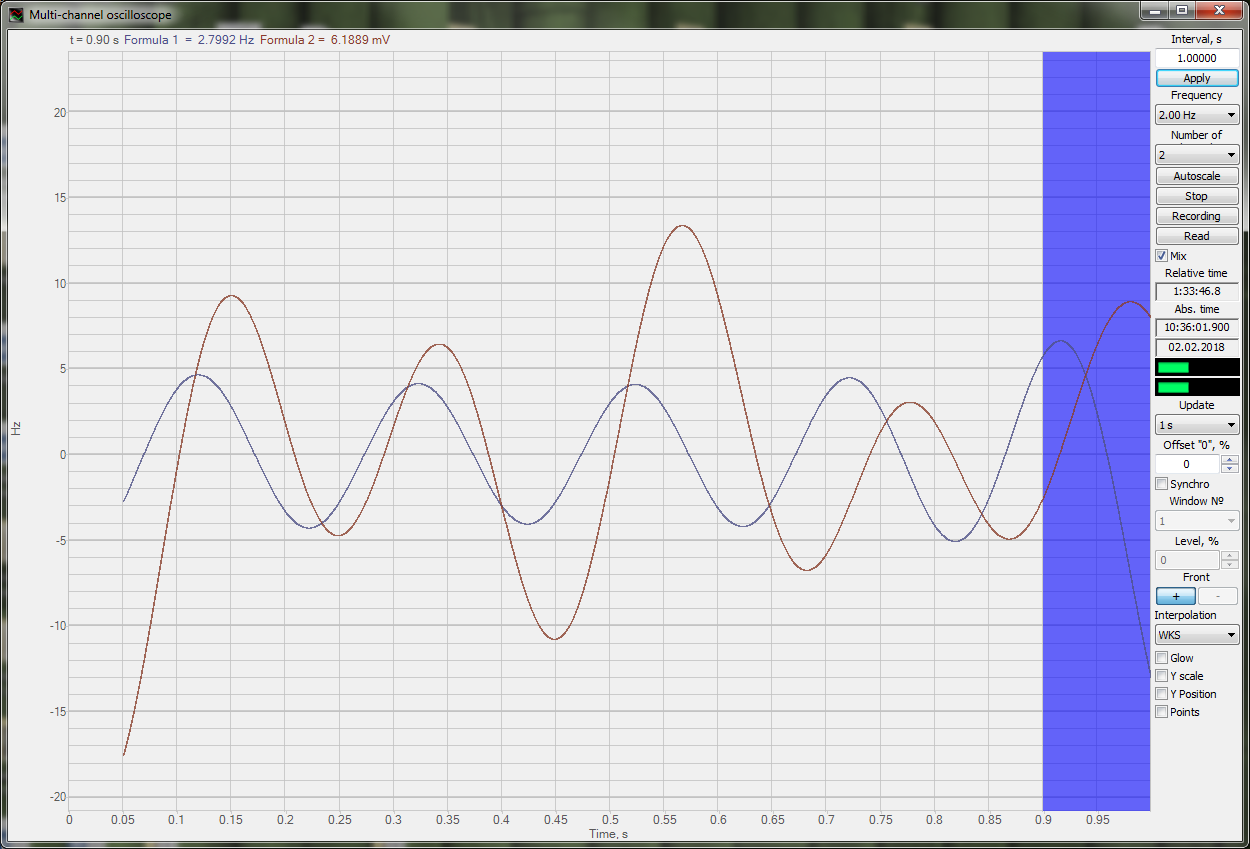
The figure below shows the operation of TimeShift function. As a source signal, there is used a function SinGen (Formula1). Timeshift is set for an interval of 0,1 s (Formula2).
ThreshD (
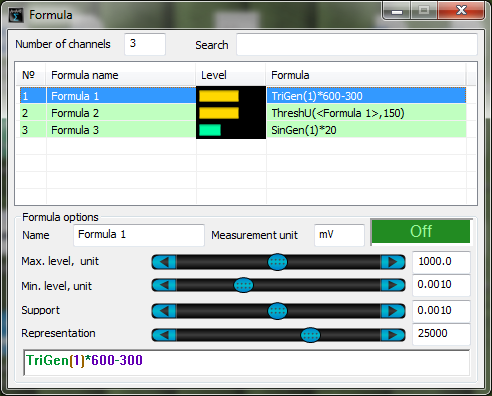
ThreshU (
in order to set a negative value as a constant, one can use postfix inversion operator.
The figure below shows a result of ThreshD and ThreshU functions operation. As a source signal, a triangular signal is used – it has an amplitude of ±300 mV (Formula 1). The bottom limit is -150 (Formula 2), the top limit: 150 (Formula 3).
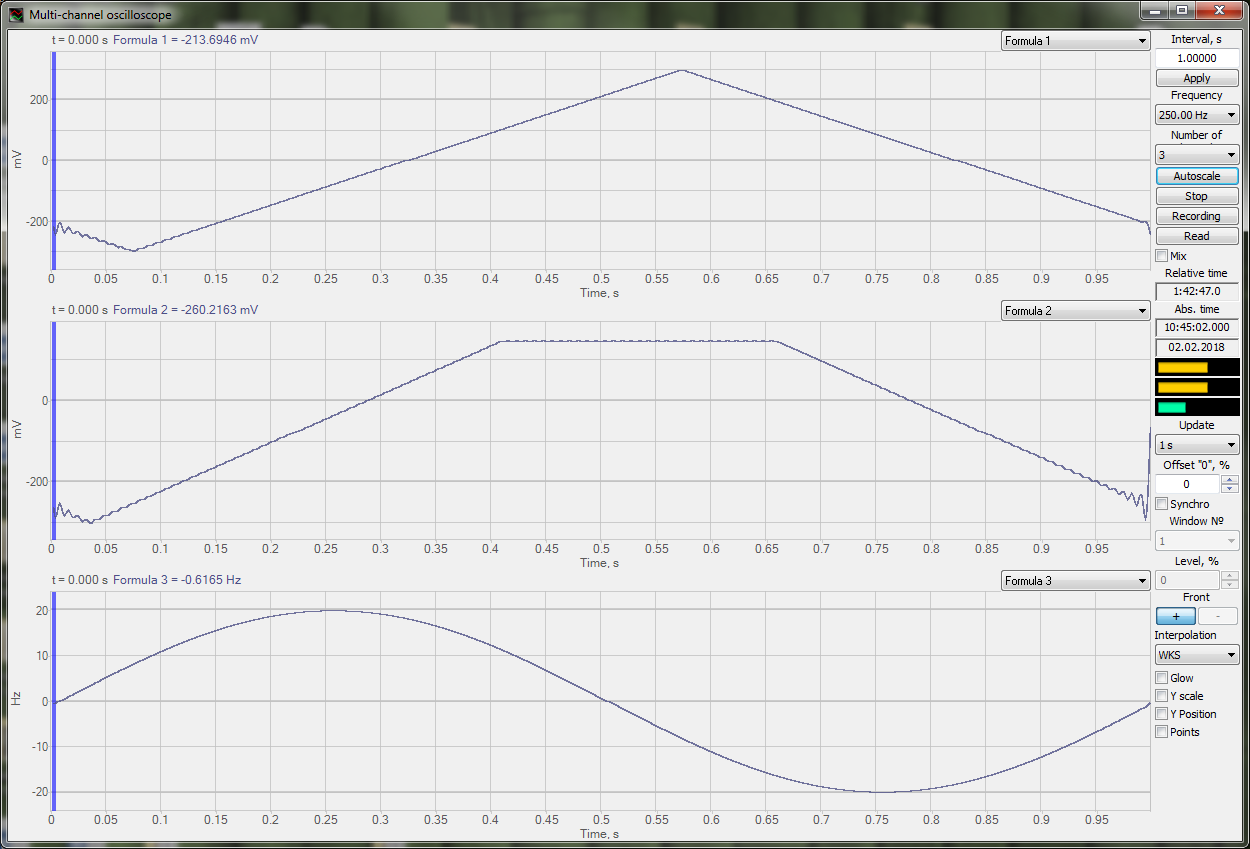
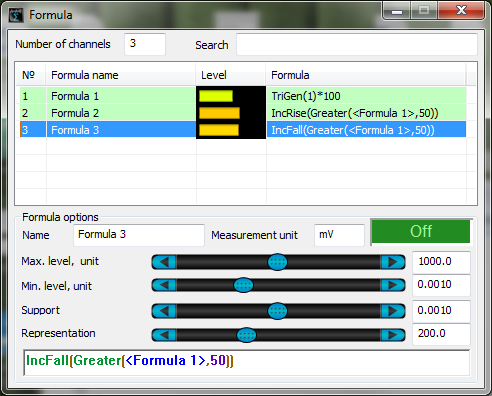
IncRise (
IncFall (
It is necessary to use the logical functions Equal and Greater. The figure below shows an example of transitions counter operation. It is based on saw-shaped signal TriGen.
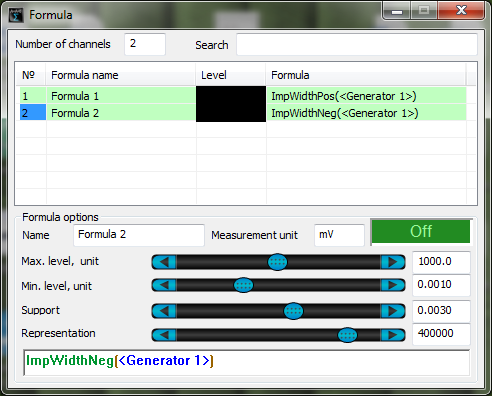
ImpWidthPos(
ImpWidthNeg(
It is necessary to use logical functions Equal and Greater.
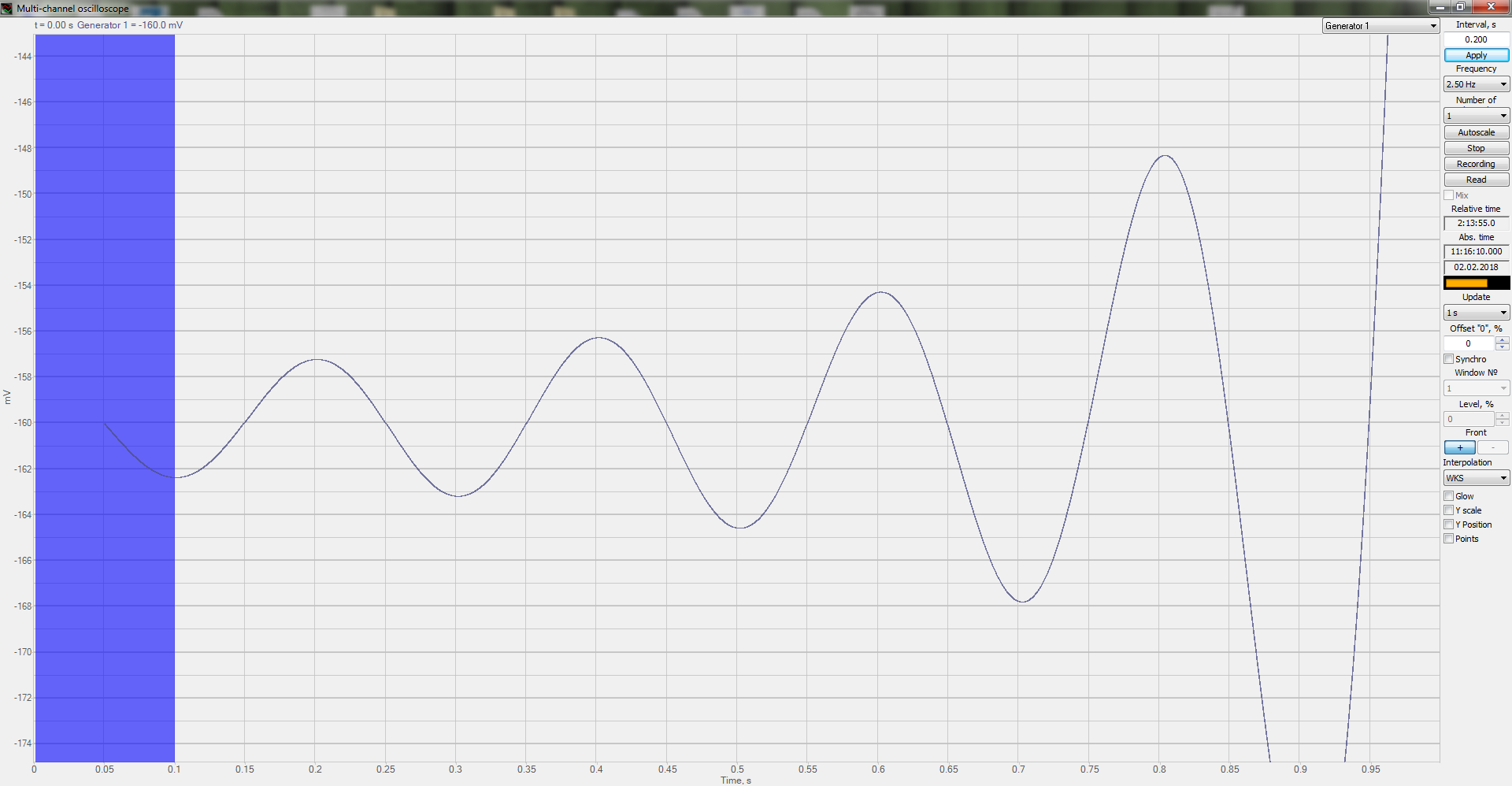
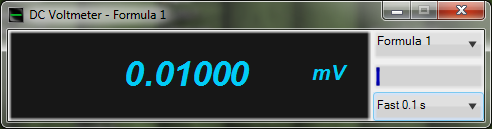
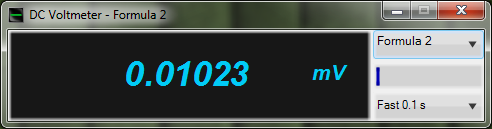
The figures below show an example of functions ImpWidthPos and ImpWidthNeg operation.