Двоичное число — компонент. Предназначен для перевода десятичного целого числа в его двоичное представление.
Внешний вид компонента
| Режим проектировщика | Режим оператора |
|---|---|
 |
Не имеет |
Параметры:
Входные
- Число — служит для перевода десятичного целого числа в двоичное представление.
Выходные
- Бит 1 — состояние младшего (0-го) бита переведенного числа;
- …
- Бит N — состояния N-го бита переведенного числа.
Настраиваемые свойства:
Общие свойства (окружение)
Частные свойства (в скобках значение, установленное по умолчанию):
- BitQuantity (1) — установка числа двоичных разрядов для перевода числа.
Программирование
При использовании компонента в сценарии и программируемом компоненте (скрипте) необходимо учитывать диапазоны значений подаваемых на входные ножки компонента, диапазоны значений свойств компонента, а также диапазоны значений параметров методов компонента.
Параметры:
Входные
- Число — двоичное представление из десятичного целого числа (любое число).
Настраиваемые свойства:
Общие свойства (окружение)
Частные свойства (в скобках значение, установленное по умолчанию):
- LONG BitQuantity — установка и чтение количества бит (от 1 до 249).
Пример
Проект в SCADA ZETView
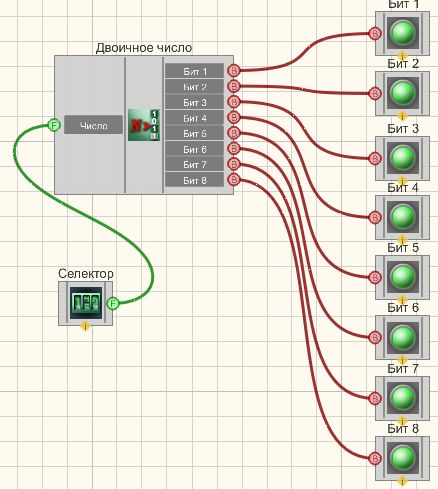
В этой схеме компонент Двоичное число служит для перевода целого десятичного числа в двоичную форму. Селектор нужен для ввода требуемого числа. Световые индикаторы служат для графического отображения двоичной формы (зеленый цвет — логическая единица, красный — ноль). Данный компонент используется для создания различных проектов, в том числе таких как анализатор спектра ZET 017 U24.
Результат работы проекта
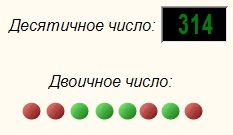
Математическое описание
Двоичная система исчисления — это позиционная система счисления с основанием 2. В данной системе число записывается только при помощи 0 и 1. Бит — один разряд двоичного кода (двоичная цифра). Двоичная система получила широкое распространение в электронике из-за ее простоты: смоделировать два состояния электронной схемы и затем их безошибочно различить неизмеримо проще, чем три, четыре и более. Восемь бит образуют байт. Это сложилось исторически, да и так удобнее: число кратно степени двойки, т.е. легко масштабируется. Шестнадцатиразрядное число – это просто два байта, тетрада (4 бита) – полубайт. Существует также двоично-десятичный код (binary-coded decimal, BCD-код). Они широко применяются в АЦП. Каждая значащая десятичная цифра в таком коде представляется четырьмя двоичными знаками и содержит десять значений сигнала от 0 до 9. Так например 13710 – это 0001 0011 0111BCD. Заметим, что такое представление не эквивалентно 13710=100010012. Очевидно, что двоично-десятичное представление не экономично с точки зрения использования разрядов, т.к. каждая группа из четырех бит способна “вместить” 16 состояний, а используется только 10 из них.
Преимущества BCD:
- упрощенный ввод-вывод чисел на индикацию;
- для дробных чисел (как с фиксированной, так и с плавающей запятой) при переводе в человекочитаемый десятичный формат и наоборот не теряется точность;
- упрощены умножение и деление на 10, а также округление.
Недостатки BCD:
- усложнены арифметические операции;
- требуется больше памяти.
Под цифровой электроникой мы подразумеваем схемы, в которых в каждой точке, как правило, можно определить только два состояния. Отсюда и такое внимание к двоичной системе исчисления. Например, транзистор открыт или закрыт. Как правило, выбирают в качестве параметра напряжение, а не ток. Отсюда и выбор уровней: Высокий и Низкий. Например для высокоскоростной КМОП логики входные напряжения от уровня земли до 1,5 В представляют как Низкий уровень, а напряжение в пределах 1,5 В до 5 В питания – как Высокий уровень. Эти состояния могут быть представлены различными битами (binary digits – двоичные разряды) информации. Например, замкнут ключ или разомкнут, есть или нет сигнала, уровень аналогового сигнала выше или ниже уровня – все это можно представить одним битом числа. Состояния Высокого и Низкого уровней определяют некоторым заданным образом “истинные” и “ложные” значения в булевой алгебре.
Большинство логических микросхем принадлежат к одной из разновидностей – ТТЛ(TTL, Транзисторно-транзисторная логика) и КМОП (CMOS, Комплиментарные [транзисторы типа] металл-окисел-полупроводник). В технологии КМОП используются полевые транзисторы с изолированным затвором с каналами разной проводимости. Отличительной особенностью схем КМОП по сравнению с биполярными технологиями (ТТЛ, ЭСЛ и др.) является:
- очень малое энергопотребление в статическом режиме (в большинстве случаев можно считать, что энергия потребляется только во время переключения состояний);
- напряжение логической единицы практически равно напряжению питания, а напряжение логического нуля практически равно потенциалу “земли” (при ненагруженных выводах);
- порог переключения практически равен половине напряжения питания;
- широкий диапазон рабочих напряжений.
Но по сравнению с ТТЛ КМОП имеет низкое быстродействие, обусловленное тем, что изолированный затвор МОП-транзистора представляет собой конденсатор довольно большой емкости. В совокупности с выходным резистивным сопротивлением, такой конденсатор образует фильтр нижних частот. В цифровой электронике важны не просто частотные свойства, а время задержки распространения сигнала на один логический элемент. Задержка возникает по причине того, что фронт сигнала не строго вертикальный, а наклонный. В связи с этим, когда сигнал на выходе начнет только нарастать (уменьшаться), в то время как на входе уже достигнет уже величины достаточной для переключения уровня. Другим следствием наличия высокой входной емкости у КМОП является то, что при переключении возникает импульс тока перезарядки этой емкости. Вследствие этого появляются затянутые фронты, отсюда элемент находится довольно длительное время в активном режиме, когда выходные транзисторы приоткрыты. В сочетании с высокоомными входами это все приводит к снижению помехозащищенности при переключениях.
