Частотная модуляция — компонент. Позволяет генерировать сигнал, создаваемый по специальному закону модуляции частоты, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.
Внешний вид компонента
| Режим проектировщика | Режим оператора |
|---|---|
 |
Не имеет |
Параметры:
Входные
- Несущая частота — частота несущего сигнала, Гц;
- Модуляционная частота — частота частотной модуляции, Гц;
- Уровень — уровень частотной модуляции, В;
- Глубина — коэффициент частотной модуляции;
- Вкл\Выкл — включение и выключение генератора.
Выходные
- Канал — канал генератора, сгенерированного по заданным параметрам сигнала.
Настраиваемые свойства:
Общие свойства (окружение)
Частные свойства (в скобках значение, установленное по умолчанию):
- CentralFrequency (1000) — частота несущего сигнала, Гц;
- ModFrequency (1) — частота частотной модуляции, Гц;
- Level (1) — амплитуда выходного сигнала, В;
- Depth (0) — глубина частотной модуляции;
- Activate (false) — состояние подачи сигнала (подан или отключен);
- Number (0) — номер канала генератора, который необходимо задействовать. Если значения DeviceType и SerialNumber не равны 0, но выбор идёт среди каналов заданного устройства. Если такого устройства в системе нет или значения DeviceType или SerialNumber равны 0, то выбор идёт среди всех доступных каналов всех устройств;
- DeviceType () — тип устройства: ZET 210; ZET 220; ZET 230; ZET 240; ZET017-U2; ZET017-U4/8, генератор которого необходимо задействовать;
- SerialNumber (0) — серийный номер устройства, генератор которого необходимо задействовать.
Программирование
При использовании компонента в сценарии и программируемом компоненте (скрипте) необходимо учитывать диапазоны значений подаваемых на входные ножки компонента, диапазоны значений свойств компонента, а также диапазоны значений параметров методов компонента.
Параметры:
Входные
- Несущая частота — значение выходного значения частоты несущего сигнала (число);
- Модуляционная частота — значение выходного частоты частотной модуляции (число);
- Уровень — значение амплитуды выходного сигнала, В (число);
- Глубина — значение глубины частотной модуляции (число).
Настраиваемые свойства:
Общие свойства (окружение)
Частные свойства (в скобках значение, установленное по умолчанию):
- FLOAT CentralFrequency — установка и чтение частоты несущего сигнала (от 0.01 до максимально допустимого уровня сигнала ЦАП), Гц;
- FLOAT ModFrequency — установка и чтение частоты частотной модуляции (от 0.01 до максимально допустимого уровня сигнала ЦАП), Гц;
- FLOAT Level — установка и чтение уровня сигнала (от 0 В до максимально допустимого уровня сигнала ЦАП);
- FLOAT Depth — установка и чтение глубины частотной модуляции (от 0 до 1);
- VARIANT_BOOL Activate — установка и чтение состояния наличия сигнала:
- true — состояние наличия сигнала включено;
- false — состояние наличия сигнала выключено.
- LONG Number — установка и чтение номера генератора в системе (от 0 до (количество генераторов — 1));
- BSTR DeviceType — установка типа устройства: ZET 210; ZET 220; ZET 230; ZET 240; ZET017-U2; ZET017-U4/8 (строка);
- LONG SerialNumber — установка и чтение серийного номера устройства (число).
Пример
Проект в SCADA ZETView
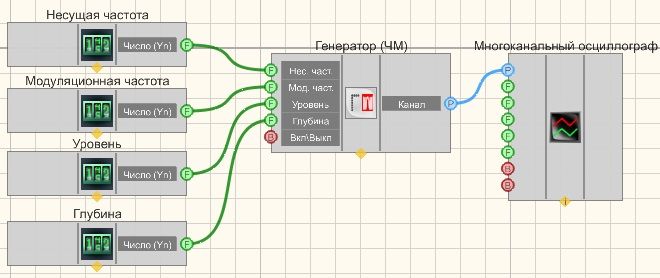
В этой схеме компонент Частотная модуляция на несущей производит частотное модулирование сигнала. Селекторы служат для задания несущей и модуляционной частот, уровня, глубины. Многоканальный осциллограф нужен для визуального представления смодулированного сигнала. Данный компонент используется для создания различных проектов, в том числе таких как акселерометр пьезоэлектрический серии 4326 а.
Результат работы проекта
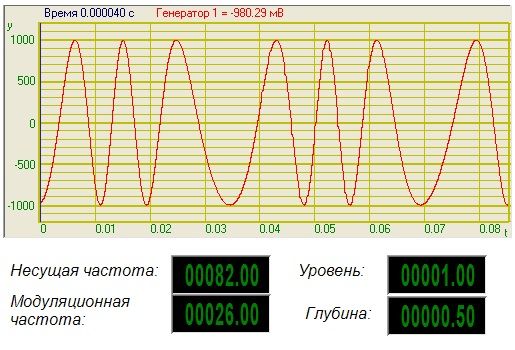
Математическое описание
Фазовая и Частотная модуляция сигнала заключаются в изменении частоты или фазы ВЧ колебания по закону управляющего сигнала. ЧМ была известна в 20х годах, но практическое применение получила с середины 30х годов, с развитием техники УКВ связи. В настоящее время ЧМ широко используется в коммерческой радиосвязи, радиовещании на метровых волнах и телевидении для передачи звукового сопровождения и т.д. Как известно, периодические колебания можно выразить уравнением: ![]() ,
,
Где φ — фаза колебания, характеризующая состояние колебательного процесса в данный момент времени, ω0 — частота ВЧ колебаний. Фаза является функцией времени и связана с частотой зависимостью: ![]() .
.
В свою очередь: ![]() .
.
Взаимная зависимость фазы и угловой частоты такова, что всякое отклонение фазы от линейного закона приводит к отклонению частоты от начального значения и наоборот. По этим причинам при ФМ всегда меняется частота, а при Частотной модуляции – фаза.
Несмотря на их тесную связь, частотную и фазовую модуляции можно различать по тому, какой из параметров (частота или фаза) находится под воздействием модулирующего фактора. Частотная модуляция намного лучше, чем амплитудная модуляция.
Если модулирующий фактор меняет фазу, то модуляцию следует считать фазовой (хотя при этом меняется и частота) и, наоборот, если модулирующий фактор меняет частоту (хотя при этом меняется фаза), то модуляцию следует считать частотной.
Рассмотрим их взаимную зависимость. При ФМ фаза меняется по закону модулирующего напряжения UΩ(t), т.е. ![]() ,
,
Где ω0t — составляющая фазы, изменяющаяся по линейному закону;
![]() — составляющая фазы, изменяющаяся по закону напряжения UΩ(t), где k – коэффициент пропорциональности.
— составляющая фазы, изменяющаяся по закону напряжения UΩ(t), где k – коэффициент пропорциональности.
В результате при модуляции по фазе: ![]() ,
,
где mφ=kUmΩ=Δφ — максимальное отклонение фазы от линейного закона или индекс фазовой модуляции. Индекс ФМ, как и коэффициент модуляции (при амплитудной модуляции) зависит от амплитуды низкой частоты UmΩ. Изменение фазы приводит к изменению частоты: при опережении фазы частота ω увеличивается, а при отставании фазы — уменьшается.
Закон изменения частоты при ФМ можно определить из уравнения ![]() ,
,
Где ![]() — максимальное отклонение частоты от начального значения или девиация частоты. Из этого выражения следует, что при ФМ прямой пропорциональности между девиацией частоты Δω и амплитудой модулирующего напряжения UmΩ Не соблюдается. Девиация частоты Δφ зависит от частоты Ω модуляции и различна на различных модулирующих частотах. Эта зависимость объясняется так: чем больше частота модуляции Ω, тем чаще (быстрее) меняется фаза φ и, следовательно, больше скорость изменения фазы во времени (т.е. угловая частота выше). При ЧМ частота колебаний меняется по закону модулирующего напряжения:
— максимальное отклонение частоты от начального значения или девиация частоты. Из этого выражения следует, что при ФМ прямой пропорциональности между девиацией частоты Δω и амплитудой модулирующего напряжения UmΩ Не соблюдается. Девиация частоты Δφ зависит от частоты Ω модуляции и различна на различных модулирующих частотах. Эта зависимость объясняется так: чем больше частота модуляции Ω, тем чаще (быстрее) меняется фаза φ и, следовательно, больше скорость изменения фазы во времени (т.е. угловая частота выше). При ЧМ частота колебаний меняется по закону модулирующего напряжения: ![]() , где
, где ![]() – характеризует отклонение частоты от начального значения. Величина
– характеризует отклонение частоты от начального значения. Величина ![]() — есть максимальное отклонение частоты от среднего значения или девиация частоты. В моменты максимума, т.е. +UmΩ, частота увеличивается, а в моменты минимума — UmΩ частота уменьшается. При этом меняется фаза колебаний. Определим фазу колебаний для частотной модуляции:
— есть максимальное отклонение частоты от среднего значения или девиация частоты. В моменты максимума, т.е. +UmΩ, частота увеличивается, а в моменты минимума — UmΩ частота уменьшается. При этом меняется фаза колебаний. Определим фазу колебаний для частотной модуляции: ![]() .
.
Полагая для упрощения φ0 = 0, получим: ![]() ,
,
Где ![]() — максимальное отклонение фазы от линейного закона или индекс частотной модуляции. Следовательно, как видим, из выше приведенной формулы для φ – фаза колебаний при частотной модуляции меняется по иному закону, чем частота и не пропорциональна амплитуде модулирующего напряжения UmΩ. На основании уравнения при ЧМ колебания можно представить следующим образом:
— максимальное отклонение фазы от линейного закона или индекс частотной модуляции. Следовательно, как видим, из выше приведенной формулы для φ – фаза колебаний при частотной модуляции меняется по иному закону, чем частота и не пропорциональна амплитуде модулирующего напряжения UmΩ. На основании уравнения при ЧМ колебания можно представить следующим образом: ![]() .
.
Форма ЧМ сигнала внешне похожа на ФМ колебания. Однако, законы изменения частоты в них различны. Так, если фаза меняется по закону sin Ωt, то частота – по закону cos Ωt и наоборот.
