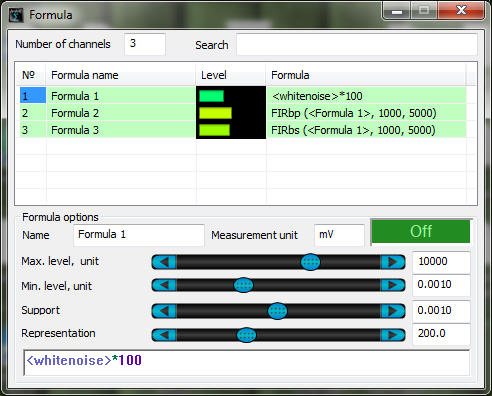
Filtros
Programa Fórmula
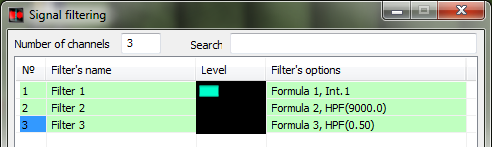
El menú Filtros contiene funciones que superponen distintos filtros:
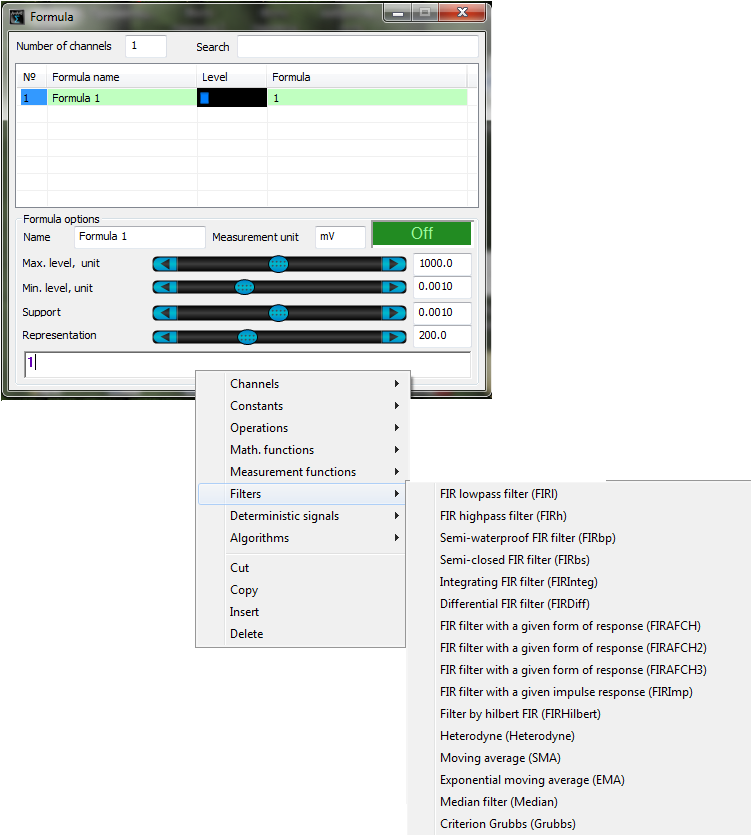
Algunos detalles sobre el uso de los filtros con la característica de impulso final
Los filtros con la característica de impulso final tienen un retraso definido por la cantidad de factores. Además, el retraso es siempre igual al número de coeficientes del filtro. También el número de coeficientes sirve como medida de la precisión del filtro: relación de la frecuencia de discretización por canal relacionada al número de coeficientes del filtro representa la mitad de la línea de frecuencias en la que el filtro cumple con los requisitos. En general, para un filtro digital en gran número de casos es mejor aumentar el número de factores. Pero hay una limitación importante: con un gran número de factores el filtrado de la señal ocupa demasiado tiempo del procesor. Por lo tanto, en el programa Fórmula está introducido un algoritmo para calcular la cantidad óptima de factores.
El número de coeficientes del filtro se calcula según el siguiente algoritmo:
1) se determina la frecuencia de tacto del procesador instalado, y el número de factores se calcula de tal manera que la carga de un núcleo del procesador sea de 3%. Fórmula para el cálculo:
tapslen = CPUSPEED*2%/ADC_FREQUENCY,
donde tapslen es el número de coeficientes del filtro,
CPUSPEED es la frecuencia de tacto del procesador, Hz,
ADC_FREQUENCY — frecuencia de discretización por el canal filtrado.
2) Si el resultado obtenido supera el número racionalmente admisible de coeficientes (2000), entonces el número de coeficientes se equipara a este resultado.
3) Si el resultado es inferior al mínimo permitido (20), el número de coeficientes se equipara a este resultado.
4) Si el resultado obtenido no permite calcular el resultado con la precisión requerida por la frecuencia, se utiliza la fórmula:
tapslen = 1/(0.5*NORM_FREQ),
donde NORM_FREQ es la frecuencia normalizada, es decir, frecuencia introducida relacionada a la frecuencia de discretización.
5) Si el resultado es demasiado costoso por la potencia de cálculo (carga más de 30% de un núcleo del procesador), entonces el resultado final se calculará por la fórmula:
tapslen = CPUSPEED*30%/ADC_FREQUENCY.
Ejemplo:
Supongamos que se requiere calcular el retraso temporal por el canal con una frecuencia de discretización 500 kHz en un procesador con doble núcleo de 2.5 GHz, al imponer un filtro de frecuencias inferiores a 300 Hz.
Usaremos el algoritmo paso a paso:
1) tapslen = 2.5 e+9 * 2e-2 / 5e+5 = 100 — opción en la que la carga del procesador será 2% dividida por el número de núcleos, es decir, el 1%
2), 3) — no afectan el resultado
4) tapslen = 1 / (5e-1 * 3e+2 / 5e+5) = 3.3 e+3 — este número de coeficientes se necesita para realizar la tarea necesaria
5) tapslen = 2.5 e+9 * 3e-1/ 5e+5 = 1500 — nos podemos permitir tal cantidad de factores bajo estas condiciones.
Ahora, cuando se ha recibido el número de coeficientes del filtro tapslen = 1500, vamos a evaluar el retardo temporal y en que medida el filtro requerido cumple con nuestros requisitos de precisión.
El retraso temporal dt = tapslen/ADC_FREQUENCY = 1.5 e+2 / 5e+5 = 3e-4 (segundos), o de 300 mks.
La frecuencia de corte del filtro será de: F de corte = ADC_FREQUENCY/(0.5 e-1 * tapslen) = 5e+5 / ( 0.5 e-1 * 1.5 e+3) = 6.7 e+3 (Hz), es decir, dos veces más de lo requerido.
¡Sea atento! Con altas frecuencias de discretización no vale la pena configurar los filtros con precisión demasiado alta — Usted cargará el procesador pero no logrará obtener resultado. Intente elegir para las mediciones el rango de frecuencia más óptimo. Si Usted necesita investigar la señal de frecuencias altas, le aconsejamos utilizar un oscilador heterodino de aparato.
Nota: en el programa Filtrado de señales se utilizan filtros con característica de impulso interminable. Al describir los filtros Fórmulas aparecerán los resultados de funcionamiento de filtros del programa Filtrado de señales – para la comparación.
Descripción de filtros
FIRl(<canal>, const) – filtro de frecuencias bajas con una frecuencia de límite igual a const. La frecuencia no puede ser menos de cero y más de la mitad de la frecuencia de discretización. Este tipo de filtro se debe utilizar para el recorte de componentes no deseados de alta frecuencia, por ejemplo — en la tarea de identificación de movimiento de una persona o un vehículo por la tierra, donde la señal que nos interesa se encuentra en el área de bajas frecuencias.
FIRl(<canal>, const) – filtro de frecuencias altas con una frecuencia de límite igual a const. La frecuencia no puede ser menos de cero y más de la mitad de la frecuencia de discretización. Este tipo de filtro se debe utilizar para el recorte de las componentes constante y de baja frecuencia de la señal. Ejemplo de uso: lectura de salida de la información de sonido con recorte de una parte inaudible y de la componente constante.
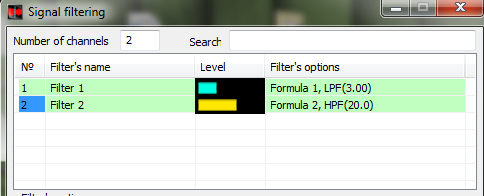
En las siguientes figuras se muestra un ejemplo de filtrado de la señal de ruido (se utiliza la función de la fórmula ) con un filtro de frecuencias bajas y un filtro de frecuencias altas en el programa Fórmula y en el programa Filtrado de señales.
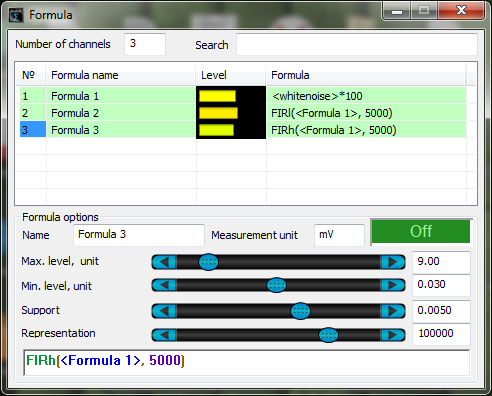
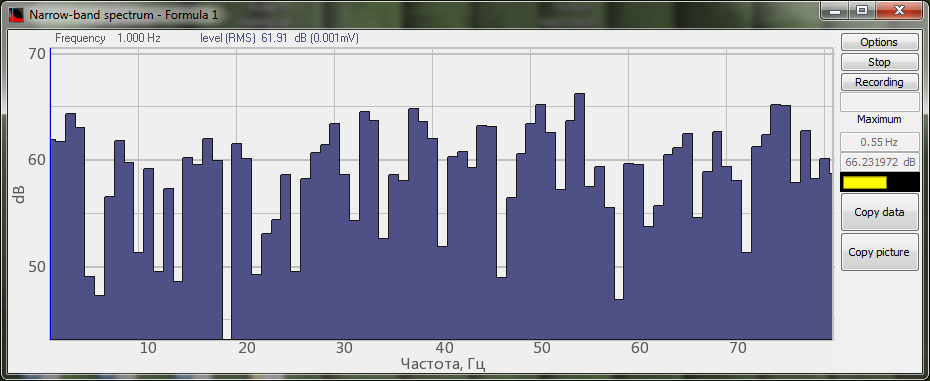
El espectro de la señal original
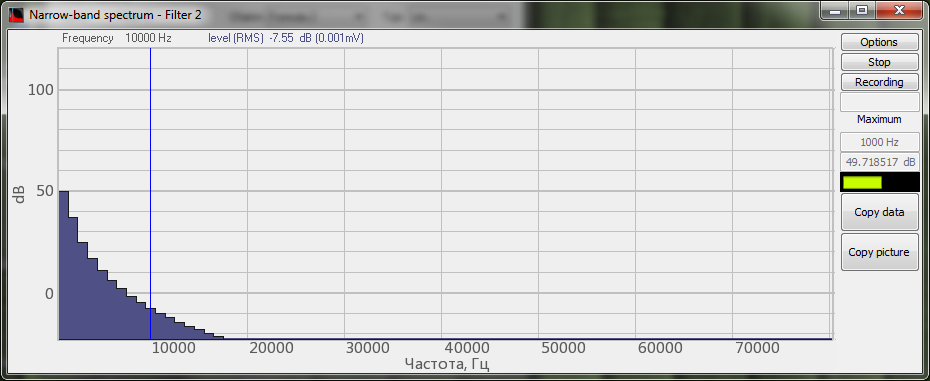
Espectro de la señal procesada por el filtro de frecuencias inferiores del programa Fórmula
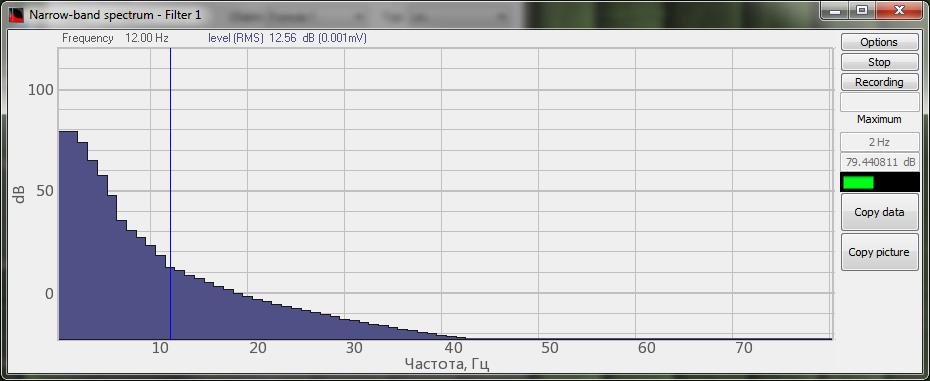
El espectro de la señal procesada por el filtro de frecuencias superiores del programa Fórmula
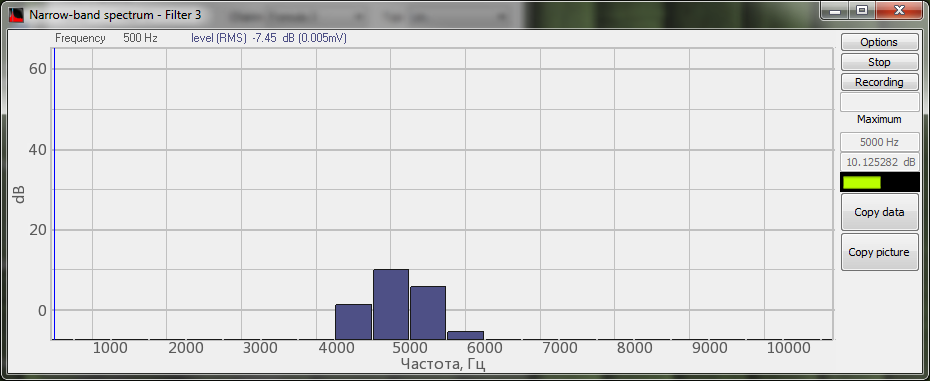
Espectro de la señal procesada por el filtro de frecuencias inferiores del programa Filtrado de señales
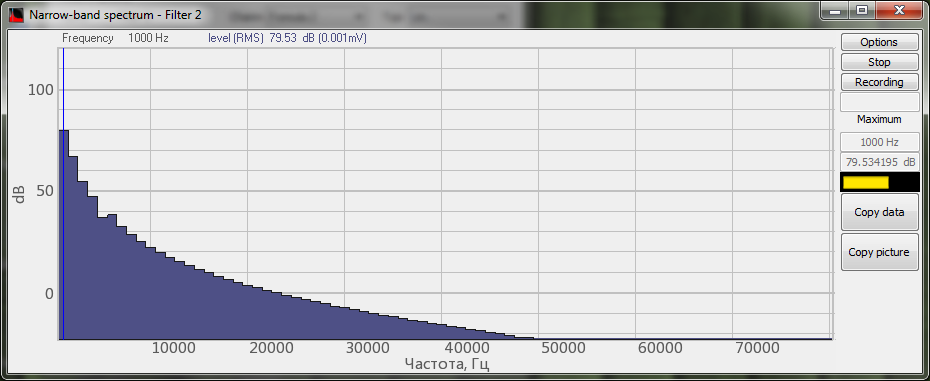
El espectro de la señal procesada por el filtro de frecuencias superiores del programa Filtrado de señales
FIRbp(<canal>, const 1, const 2) – filtro de banda que deja pasar las frecuencias desde la primera hasta la segunda. Los valores de frecuencias no pueden ser menos de cero y más de la mitad de la frecuencia de discretización. Si se han introducido tales valores, entonces el filtro en su lugar pone los máximos permitidos. El filtro puede ser utilizado para cortar las frecuencias que corresponden a la voz humana.
FIRbp(<canal>, const 1, const 2) – filtro de banda que recorta las frecuencias desde la primera hasta la segunda. Los valores de frecuencias no pueden ser menos de cero y más de la mitad de la frecuencia de discretización. Si se han introducido tales valores, entonces el filtro en su lugar pone los máximos permitidos. En la frecuencia no hay diferencia en el orden de las frecuencias.
En las siguientes figuras se muestra un ejemplo de filtrado de la señal de ruido (se utiliza la función de la fórmula ) con un filtro de paso de banda y un filtro de obstrucción de banda en el programa Fórmula y en el programa Filtrado de señales.
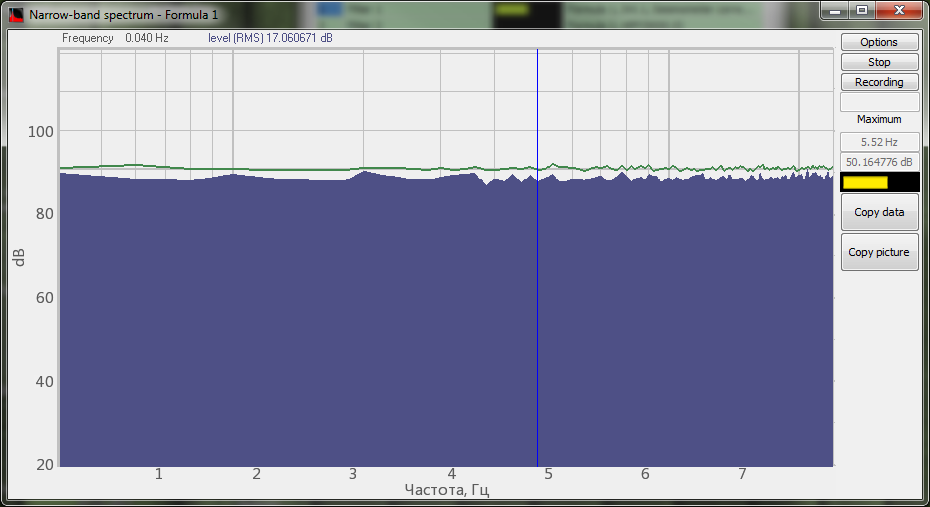
El espectro de la señal original
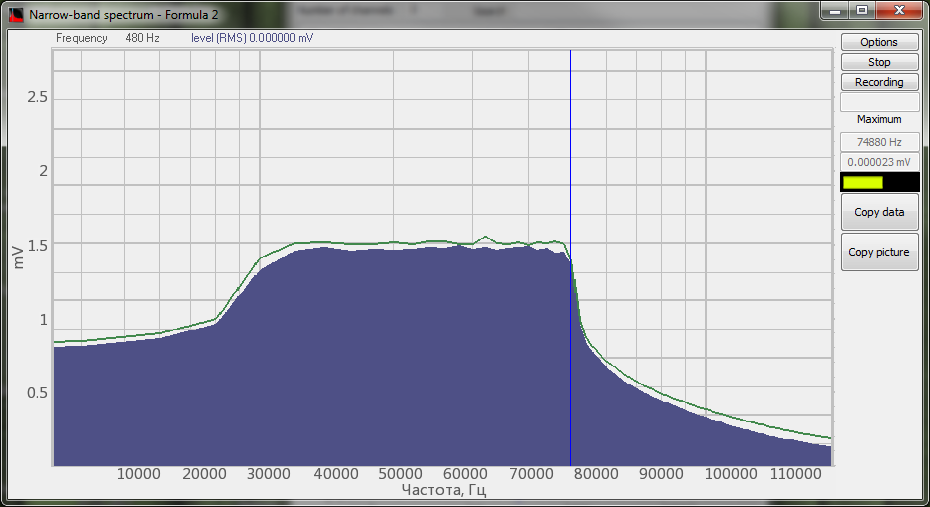
Espectro de la señal procesada por el filtro de paso de banda del programa Fórmula
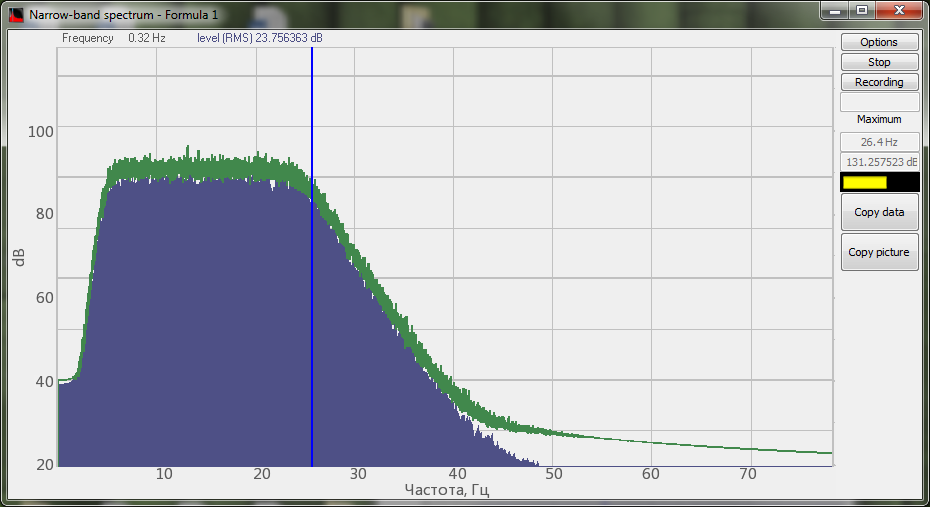
Espectro de la señal procesada por el filtro de obstrucción de banda del programa Fórmula
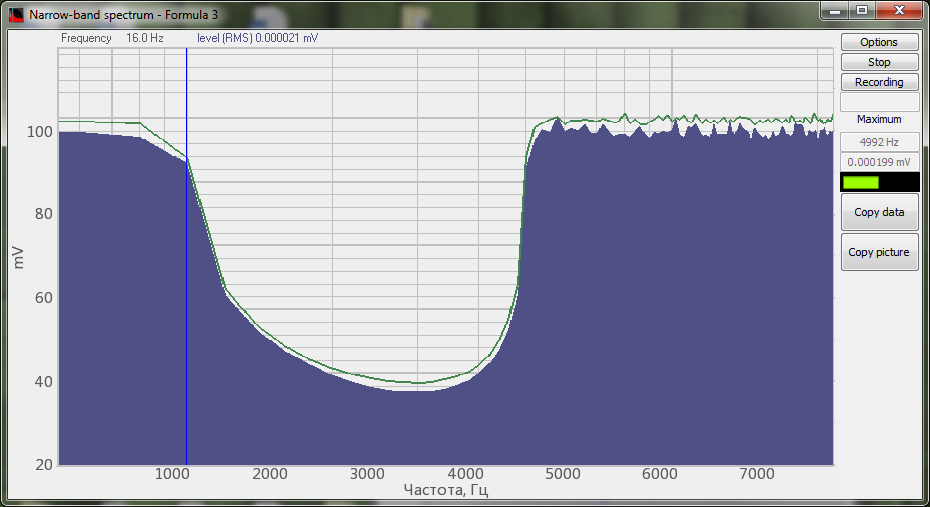
Espectro de la señal procesada por el filtro de paso de banda del programa Filtrado de señales
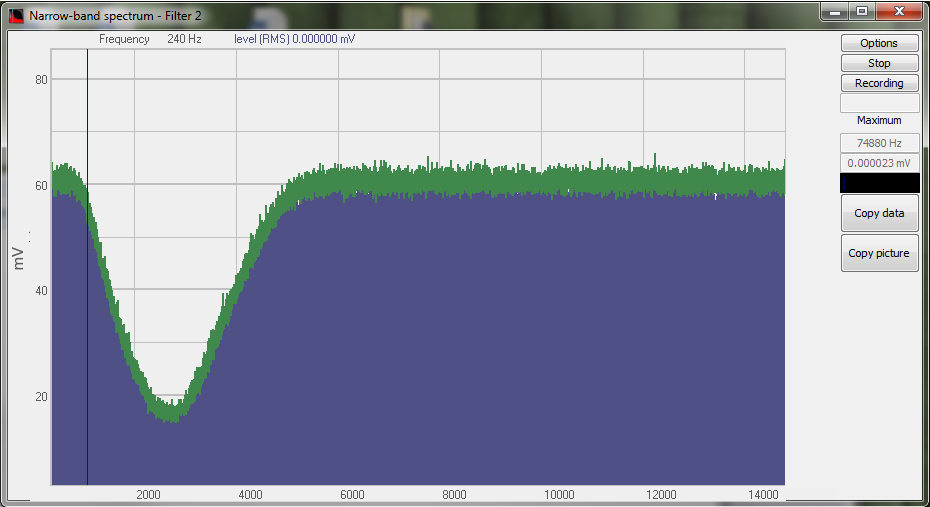
Espectro de la señal procesada por el filtro de obstrucción de banda del programa Filtrado de señales
FIRInteg(<canal>) – filtro con característica de impulso final integrante es potencialmente inestable, por lo tanto antes de su uso hay que poner un filtro de frecuencias altas.
FIRDiff(<canal>) — filtro diferenciador con característica de impulso final
FIRAFCH(<canal1>, <canal2>) – filtro con característica de impulso final con la forma de característica de amplitud y frecuencia especificada.
Heterodyne(<canal>, frecuencia, banda) – oscilador heterodino. Corta del espectro de la señal la banda con la frecuencia Frequency Hz y la banda Ban Hz. A continuación, se desplaza a la zona de frecuencias bajas. El principal uso del oscilador heterodino es la demodulación de frecuencia de la señal, o sea proceso de transferencia de una parte del espectro de la zona de frecuencias altas a la zona de inferiores. Se aplica en tareas radiotécnicas.
SMA(<canal1>, tiempo) — filtra los promedios móviles cuyos valores promedios en cada punto de determinación son iguales al valor promedio de la función inicial por el período anterior. Los promedios móviles normalmente se utilizan con los datos de series de tiempo para la alineación de fluctuaciones a corto plazo. El promedio matemáticamente móvil es uno de los tipos de convolución, y por lo tanto puede considerarse como filtro de frecuencias bajas utilizadas en el procesamiento de las señales. Ya que en el cálculo del promedio móvil el valor de la función se calcula cada vez de nuevo, en este caso se tiene en cuenta el conjunto significativo finito de los valores anteriores, el promedio móvil «se desplaza» (se mueve) como si estuviera «moviéndose» por la serie temporal (Más detalles).
EMA(<canal1>, constante) — filtra el promedio exponencial. En un promedio móvil exponencial se cometen a alineación los valores de la función inicial, sin embargo, a la alineación también pueden ser sometidos y los valores de la función resultante. El valor «Constante» debe variar de 0 a 1, mientras menor es, más grande es el valor exponencial (Más detalles).
Median(<canal1>, Time) — un procedimiento eficaz para el procesamiento de señales expuestas a la influencia de interferencias de impulso. Es un tipo de filtros digitales ampliamente utilizado en el procesamiento digital de señales e imágenes para reducir el nivel de ruido. El filtro de mediación es un filtro no lineal con característica de impulso final. Los valores de cuentas dentro de la ventana del filtro se colocan en orden accedente (descendente); y el valor que se encuentra en el medio de la lista ordenada, llega a la salida del filtro. En el caso de un número par de cuentas en la ventana el valor de salida del filtro es igual al valor promedio de dos cálculos en la mitad de la lista ordenada. La ventana se desplaza a lo largo de la señal filtrada y los cálculos se repiten (Más detalles).
Grubbs(<canal1>, Time, Q) — excluye errores graves. Para excluir errores graves se utiliza el criterio de Grabbs. El criterio estadístico de Grabbs de exclusión de errores graves está basado en la suposición de que el grupo de resultados de mediciones pertenece a una distribución normal (Más detalles).
También le va a interesar…
• Programa Fórmula
• Canales (en el programa Fórmula)
• Constantes (en el programa Fórmula)
• Operaciones (en el programa Fórmula)
• Funciones matemáticas (en el programa Fórmula)
• Funciones de medición (en el programa Fórmula)
• Señal determinada (en el programa Fórmula)
• Algoritmos (en el programa Fórmula)
