Ударный спектр и добротность колебательной системы
Ударный спектр — это график значений максимального отклика на внешнее воздействие системы резонаторов с одной степенью свободы, упорядоченный по собственным частотам резонаторов.
Определение краткое и достаточно точное, но почему-то у людей возникают дополнительные вопросы. Дополнительные вопросы возникают оттого, что людям трудно представить себе образ даже одного резонатора с одной степенью свободы, то что говорить о целой системе.
Если объяснять этот термин на пальцах, то надо подходить к этому вопросу аккуратно и последовательно, чтобы постепенно сложить в голове человека образ описываемого явления. С материальными объектами проще — их достаточно показать, чтобы человеку всё стало ясно. С информационными явлениями гораздо сложнее, но мы эту проблему решим.
Резонатор с одной степень свободы
Представим себе объект, который может совершать колебания в пространстве только в направлении одной оси. Это и будет резонатор с одной степенью свободы. Пружины и маятники — это всё примеры резонаторов с одной степенью свободы. Хотя природа их колебаний различна в теории они описываются аналогичными уравнениями. У них есть одна собственная частота и одна резонансная частота. Для удобства практического использования эти частоты объединяют в одну, но это две разные частоты. Резонансная частота — это частота действия внешней силы, на которой достигается максимальная амплитуда колебаний. Собственная частота — это частота затухающих колебаний, когда внешняя сила исчезла и система теряет энергию, возвращаясь в положение равновесия (останавливается).

Представим себе знакомый нам всем с детства маятник — качели.
Резонансная частота маятника не зависит от массы груза (то есть не разницы кто сидит на качелях хрупкая маленькая девочка или её большой тяжёлый папа), а зависит только от длины подвеса. Чем длиннее этот подвес, тем меньше резонансная частота. Чем выше качели, тем дольше период одного качания.
Ребёнок, впервые попавший на качели, поначалу прилагает много самых разных усилий с произвольной частотой, но качели почти не двигаются. Достаточно быстро он понимает темп, в котором надо делать усилия, чтобы раскачивать качели и понимает, что делать их надо в момент, когда качели замирают на одном из пиков.
Говоря сухим научным языком, когда частота действия внешней силы совпадает с частотой резонанса система начинает в этот самый резонанс входить, увеличивая амплитуду колебаний.

Сил у ребёнка немного и раскачать качели он сильно не может. В определённый момент все силы его начинают уходит не на увеличение амплитуды колебаний, а на поддержание колебаний на том же уровне. В этот момент вся энергия, которую прикладывает ребёнок, будет тратиться за один период колебаний на преодоление трения подвеса и сопротивление воздуха. Если предположить, что в каждый период колебаний качелей ребёнок прикладывает одинаковое усилие совершая работу A, то достигнув максимальных колебаний за n раз, он затратит количество энергии:
W=n×A,
которая перейдёт в энергию качания качелей (часть этой энергии будет рассеяна, но пока это не существенно).
После этого вся его энергия будет полностью рассеиваться за один такт качения:
A=E×d
После понимания этого момента можно переходит к понятию добротности.
Добротность
Добротность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. В общем виде для любой колебательной системы добротность вычисляется по следующей формуле:
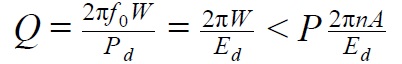
f0 — резонансная частота;
W — запасённая энергия системы;
Pd — рассеиваемая мощность;
Ed — рассеиваемая энергия за один период колебаний;
A — работа, совершаемая внешней силой за один период колебаний;
n — количество колебаний, которое сделал система, прежде чем достигла максимальной амплитуды колебаний.
Из этой формулы можно сделать один очень важный вывод, который нам пригодится:
Чем выше добротность колебательной системы, тем больше колебаний сделает система под действием внешний силы, прежде чем достигнет максимальной амплитуды.
То есть, чем выше качели (чем длиннее маятник — тем выше его добротность) тем больше нужно сделать колебаний, чтобы их раскачать. От величины внешней силы зависит только амплитуда колебаний, которые может совершать система. Если ребёнок не сам качается на качелях, а его качает папа (а у папы силы больше и энергии он даёт больше), качели будут подниматься гораздо выше, но максимальной амплитуды качели достигнут примерно за то же число колебаний, если папа будет качать с одинаковым усилием. В качании на качелях самое главное не переусердствовать иначе ребёнка может укачать или качели сломаются.
Собственная частота
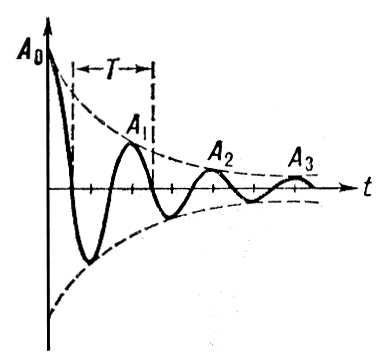
Когда дети становятся старше, им надоедает просто качаться на качелях и они раскачавшись прыгают с них, стараясь подлететь повыше и подальше приземлиться (хорошо что детские площадки посыпают песком). После такого прыжка на качелях не остаётся источника внешней толкающей силы, да и отцу становится «не очень интересно » толкать пустые качели. Постепенно амплитуда качения уменьшается и качели останавливаются. Интервал времени между двумя ближайшими моментами отклонения качелей (маятника, резонатора, сигнала и т.д.) называется периодом собственных колебаний, а обратная ему величина — частотой собственных колебаний.
Одни колебательные системы останавливаются быстро, всего за пару тройку колебаний (большинство качелей во дворе останавливаются не более чем за 7 колебаний), а колебания других могут затухать очень долго (колокола — это тоже колебательные системы). Скорость, с которой колебания затухают, очень важный параметр. Он называется декремент затухания.
Декремент затухания
Декремент затухания или логарифмический декремент колебаний — это безразмерная физическая величина, описывающая уменьшение амплитуды колебательного процесса и равная натуральному логарифму отношения двух последовательных (или через некоторое целое количество периодов) амплитуд колеблющейся величины в одну и ту же сторону:
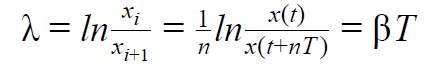
Декремент затухания равен показателю экспоненты в законе затухающих колебаний:
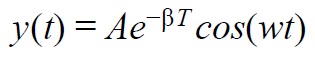
Из декремента затухания можно рассчитать другую величину — коэффициент демпфирования по следующей формуле:
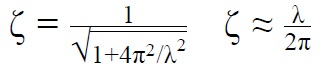
Коэффициент демпфирования (затухания)
Декремент затухания величина расчётная и рассчитывается по графику затухающих колебаний. Для колебательных систем с вязким трением (сила сопротивления пропорциональная скорости движения) физической величиной определяющей характер колебаний является коэффициент демпфирования.
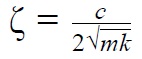 , где
, где
c — коэффициент силы сопротивления движению;
k — коэффициент упругости;
m — масса подвижного груза.
При коэффициенте демпфирования меньшем единицы колебательная система будет плавно затухать. Чем меньше будет коэффициент, тем дольше будут длиться колебания. При коэффициенте равном единице или большем никаких колебаний система испытывать не будет, а просто плавно будет стремиться к нулевому положению. Так, например, дверные доводчики настраивают на коэффициент демпфирования 1 и более, чтобы дверь автоматически закрылась через некоторое время без удара о створку. Демпферы для входных дверей в метро наоборот настроены на коэффициент демпфирования меньше 1. После того как человек толкнёт такую дверь она сделает два три колебания и остановится.
Коэффициент демпфирования связан с добротностью следующей формулой:
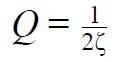
Из формулы следует, что чем больше добротность колебательной системы, тем меньше декремент затухания. Чем меньше декремент затухания, тем меньше теряется энергии с каждым колебанием и тем больше колебаний совершит система перед остановкой. Этот простой вывод нам пригодится для дальнейшей работы.
Если рассматривать качели, маятники и прочие системы с низкой собственной частотой (и большим периодом колебаний соответственно), то считать количество колебаний достаточно легко. Но когда мы рассматриваем колокола, балки и прочие системы с высокой собственной частотой, то «на глаз» подсчитать количество колебаний при затухании становится невозможно.
Система резонаторов
Если собрать несколько резонаторов с разными собственными частотами, но одинаковыми значениями декремента затухания, то получится та самая система резонаторов, о которой шла речь в самом начале статьи. Представьте себе площадку в парке отдыха, на которой установлены качели разных размеров, но похожие по конструкции. От размеров качелей будет зависеть собственная частота, а от конструкции и материалов декремент затухания. Таким образом, у них будут разные собственные частоты и одинаковый декремент затухания.

Если представить себе, что все качели одновременно испытывают воздействие внешней возбуждающей силы, от которой они начинают раскачиваться, то максимальная амплитуда колебаний, которую в какой-то момент достигнут качели, будет тем самым максимальным откликом. Подобным внешним воздействием может быть землетрясение. Если упорядочить значения максимальных ответов по возрастанию собственных частот соответствующих резонаторов, то полученный график называется ударным спектром. Если мы имеем дело с землетрясением, то в этом случае ударный спектр называют спектром ответа.
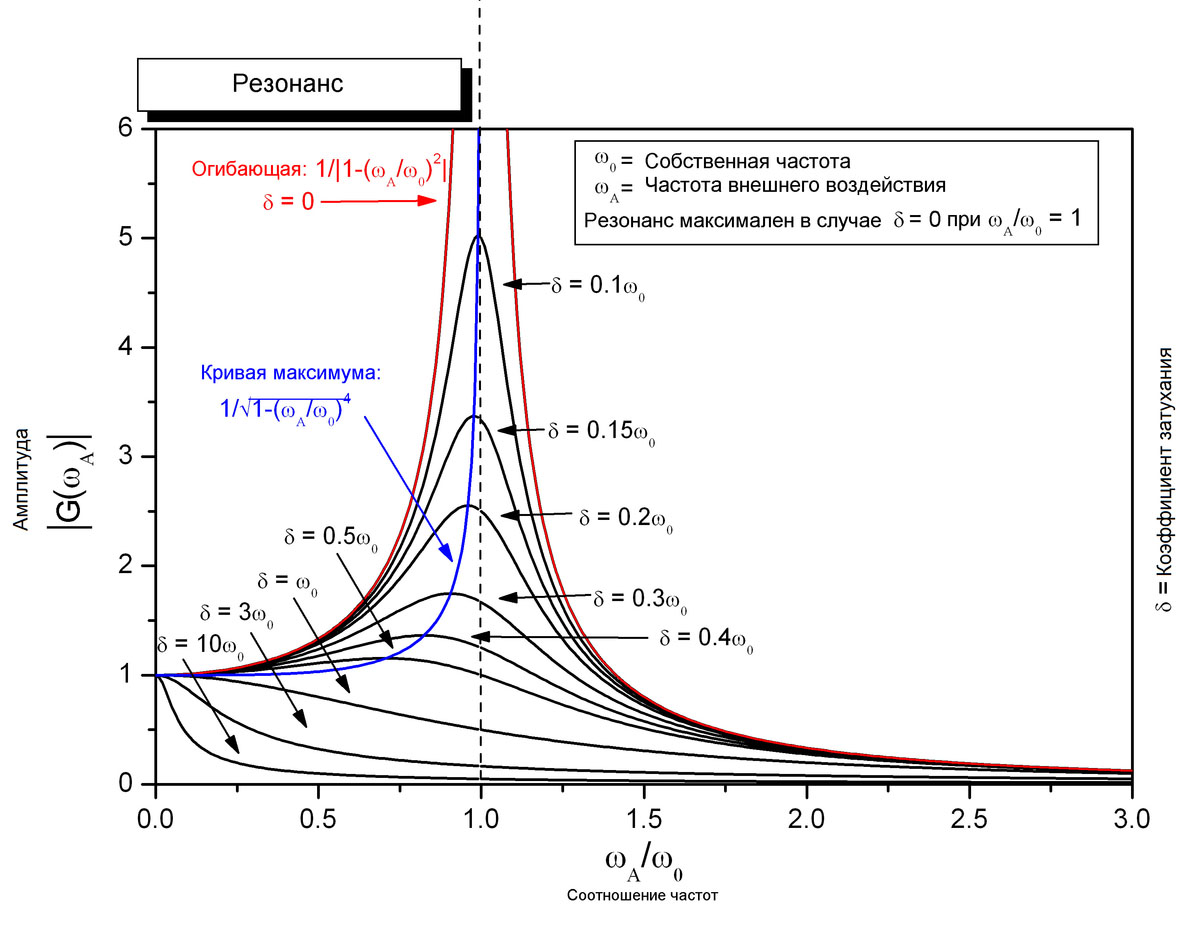
Как мы уже выяснили выше, максимальный отклик некоторых резонаторов может быть достигнут не тогда, когда мгновенное значение силы максимально, а в какой-нибудь другой момент. Этот момент зависит от гармоник, которые присутствуют в сигнале, и от их длительности. Даже если на систему действует гармонический сигнал с одной частотой, то раскачиваться под его воздействием будут все резонаторы. Максимального по амплитуде колебаний отклика достигнет резонатор с собственной частотой наиболее близкой к частоте колебаний, остальные будут колебаться меньше. Наглядно это демонстрирует график резонанса.
Если мы имеем дело, не с установившимися колебаниями, а с коротким воздействием, то картина будет иной. Будем на систему резонаторов действовать импульсом, состоящем из нескольких периодов синусоидального сигнала с частотой 1000 Гц от полу-периода до 10 периодов. Скажем заранее, что коэффициент демпфирования всех резонаторов равен 0,05, а добротность соответственно равна 10.
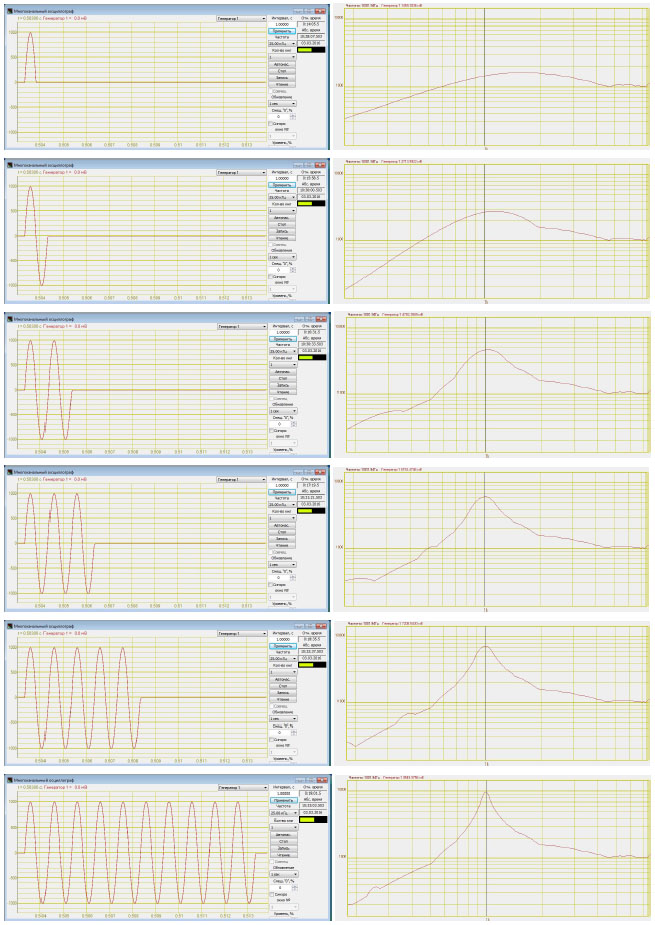
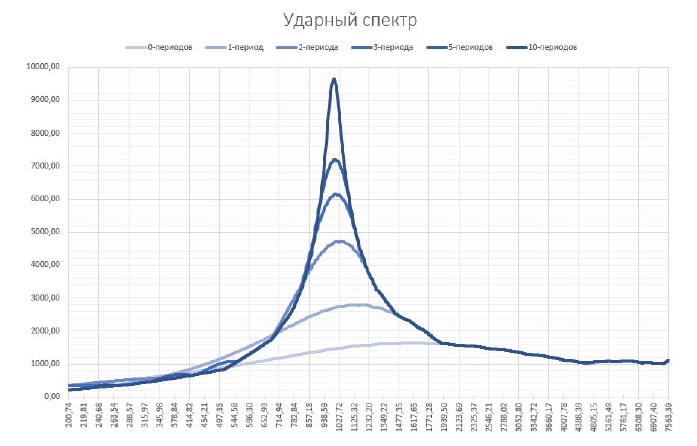
Как мы видим на графиках ударного спектра с ростом длительности воздействия увеличивается максимальный отклик системы резонаторов, причём частота, соответствующая максимальному отклику приближается к частоте сигнала генератора. На этом месте возникает уместный вопрос: «Почему от импульсов с малым числом периодов сильнее откликаются (то есть имеют большее значение) резонаторы с частотами большими частоты действующего импульса?». Для ответа на этот вопрос нужно внимательно рассмотреть график резонанса, приведённый выше.
На графике резонанса изображена зависимость ответной реакции резонатора на входное воздействие постоянной амплитуды при изменяющейся частоте входного сигнала. На графике хорошо видно, что у резонаторов с низкой добротностью резонанс наступает на частоте заметно меньшей чем собственная частота резонатора. По мере роста добротности резонатора пик резонанса становится острее и выше, а частота приближается к собственной частоте резонатора.
В ударном спектре всё наоборот. Частота входного сигнала остаётся неизменной, а варьируются собственные частоты резонаторов. Добротность каждого резонатора ограничена сверху, но длительность входного воздействия позволяет раскачать все резонаторы. Поэтому добротность каждого резонатора будет определяться количеством периодов в сигнале (но не более 10).
Если частота резонатора выше частоты входного сигнала, то соотношение wa/w0 < 1 и отклик не опускается ниже амплитуды входного сигнала. То есть маятники с коротким подвесом от низкочастотного воздействия не раскачиваются, а просто ходят за ним. Соответственно, небольшие строения (телефонные будки, ларьки и прочие) при землетрясении не испытывают внутренних напряжений и не ломаются, а двигаются все целиком за волной. Если частота резонатора ниже, то соотношение wa/w0 > 1 и амплитуда отклика быстро падает с уменьшением частоты резонатора. То есть маятники с длинным подвесом от высокочастотных воздействия даже не трогаются с места. Соответственно, большие строения (точнее сказать, строения из крупных блоков) никак не реагируют на работу отбойного молотка на улице, будь их там даже тысячи работающих одновременно.
Если взять график резонанса соответствующий δ=0.5w0, то он будет примерно соответствовать спектру ударного отклика на полу-период синуса с той лишь разницей, что он будет отражён в другую сторону. Сигналам с большим числом периодов соответствуют графики с большей добротностью. Если совместить несколько графиков ударных спектров в одних осях, то мы увидим график напоминающий график резонанса, приведённый выше, но развёрнутый в обратном направлении.
Вывод
Подводя итог статьи необходимо сделать вывод, что ударный спектр это прекрасный показатель внутреннего состояния объекта. Так для небольших объектов при построение ударного спектра по выходному сигналу можно выяснить состояние «внутренней системы резонаторов». Усталость материи, внутренние трещины и прочие неприятности вносят изменения в эту «внутреннюю систему резонаторов». Обычно это выражается в том, что происходит изменение собственных и резонансных частот, реже происходит падение добротности колебательных контуров.
Так, например, церковные колокола со временем «понижают» свои голоса, то есть у них происходит уменьшение собственной частоты (унтертона) и высота их звука падает. Таким образом проявляется эффект «старения» бронзы [1]. Если же колокол треснет (например, в сильный мороз), то он резко потеряет чистоту звука, то есть упадёт его добротность.


Можно представить себе испытуемый объект как систему резонаторов в виде набора струн (можно представить себе рояль), определить и запомнить какие «струны» в нём звучат и как сильно. А после эксплуатации по изменению этого набора откликов можно судить об внутренних изменениях. Так, например, ГОСТы на механические испытания рекомендую измерять и сравнивать АЧХ до и после испытаний. Ещё пример, при изменении основного тона собственных колебаний здания более чем в два раза в меньшую либо в большую сторону (одна из методик контроля), МЧС делает заключение, что здание находится в аварийном состоянии.
При землетрясениях наоборот измеряют ударный спектр самого землетрясения. Таким образом учёные оценивают степень разрушения зданий и сооружений [2]. Для каждого типа сооружений вычисляется диапазон наиболее разрушительных частот. Чем выше рассчитанный спектр в определённой полосе, тем больше повреждений получит здание.
При проектировании зданий в сейсмоопасных районах в конструкцию здания закладывают системы демпфирования колебаний. Системы демпфирования рассчитывают на гашение наиболее опасных частот. Такие частоты определяются исходя из анализа сейсмограмм в данной области за всё время наблюдений. И в конце проектных работы модель здания подвергают испытаниям на модельные землетрясения [3].

Ссылки
- https://www.muszone.ru/articles/23.html
- https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D0%B5%D0%BB%D1%8C_%D1%81%D0%B5%D0%B9%D1%81%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B3%D0%BE_%D0%B2%D0%BE%D0%B7%D0%B4%D0%B5%D0%B9%D1%81%D1%82%D0%B2%D0%B8%D1%8F_%C2%AB%D0%A1%D0%90-482%C2%BB
- https://ru.wikipedia.org/wiki/Сейсмостойкое_строительство
- https://www.iris.edu/hq/inclass/video/building_resonance__boss_model_construction__use
P.S.
В конце можно позволить отступить от области механики и сейсмики в область социальную. В обществе имеют место аналогичные явления, называемые «общественным резонансом». Если какое-то событие овладевает умами многих людей (говорят «нашло отклик в сердцах людей»), и о нём долго вспоминают и обсуждают (говорят «событие долго будоражит умы»), то налицо общественный резонанс. Такие события могут побудить людей к действиям, например, написать письмо на телевидение, в редакцию газеты или в руководящие органы. Руководство телеканала или администрация отсортируют письма, получат весь спектр ответов, проанализируют ситуацию и примут какие-то действия.
Подобная аналогия из жизни общества может быть не абсолютно точно повторяет свойства резонанса и ударного спектра в механике, но позволяет приблизить к пониманию механического резонанса большое число людей, не имеющих технического образования.
